back to TL-tutorial (home page)
Teil 2: Ausbreitung in linearen elektrischen Systemen
2.3.1. Bestimmungsgrößen für den Wellenwiderstand
Auf einer Doppelleitung verschiebt sich ein Puls oder eine Wellenfront mit einer bestimmten Orientierung, wenn die Spannung U und die Stromstärke I in einem bestimmten Verhältnis zueinander stehen. Dies Verhältnis wird Wellenwiderstand oder Impedanz genannt und mit Z gekennzeichnet.
Bei einem Gleichstromkreis gilt das Ohmsche Gesetz: R = U/I; bei einer Doppelleitung mit anliegender Wechselspannung gilt: Z = U/I.
Zwei Größen einer Doppelleitung - die Kapazität und die Induktivität - sind bestimmend für den Wellenwiderstand Z. Die Bedeutung dieser beiden Größen und ihr Einfluß auf den Wellenwiderstand werden im folgenden Abschnitt behandelt.
2.3.2. Kapazität einer Doppelleitung
Wie im Kapitel "2.1. Ausbreitungsvorgänge auf einer Doppelleitung" beschrieben wurde, entsteht ein Spannungspuls auf einer Leitung durch eine bestimmte Anzahl zusätzlicher Ladungsträger auf den Leiteroberflächen gegenüberliegender Abschnitte.
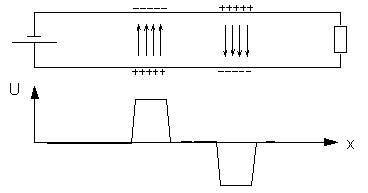
Spannungspuls und Oberflächenladungen auf einer Doppelleitung
Die Kapazität C einer Leitung steht in einem direkten Zusammenhang mit der Dichte der Oberflächenladung, die für eine vorgegebenen Spannung erforderlich ist. Je größer die Kapazität einer Leitung, desto größer ist die erforderliche Dichte an Oberflächenladungen, um eine vorgegebenen Spannung zwischen den Leitungen zu erreichen.
Es gibt zwei Möglichkeiten, die Dichte der Oberflächenladung bei vorgegebener Spannung und damit die Kapazität zu verändern. Man kann entweder den Abstand der beiden Leitungen verändern oder zwischen die beiden Leitungen ein isolierendes Material, ein sog. Dielektrikum, einbringen. Die Auswirkungen dieser beiden Möglichkeiten sind gleich: es verändert sich die Kapazität der Leitung, d. h. die Dichte der Oberflächenladungen bei gleicher Spannung.
Nähere Erläuterungen zu diesen Auswirkungen siehe unter: Abstandsänderung und Auswirkung eines Dielektrikums
Spannungspuls und Oberflächenladungen auf einer Doppelleitung
2.3.3. Induktivität einer Doppelleitung
Im Fall einer Gasströmung erscheint es plausibel, dass Gase mit unterschiedlich träger Masse einen unterschiedlichen Antrieb erfordern. Ein Gas wie Wasserstoff, dessen Moleküle achtmal leichter sind als Sauerstoffmoleküle, wird sich bei gleicher Druckdifferenz entsprechend leichter in Bewegung setzen als Sauerstoff und läßt sich auch entsprechend leichter abstoppen.
Bei einer Änderung des elektrischen Stromes, d.h. bei beschleunigten Elektronen, gibt es ebenfalls einen Trägheitseffekt, allerdings hat dieser nichts mit der trägen Masse der beweglichen Elektronen zu tun. Diese Masse ist bei allen Elektronen stets gleich - es gibt keine Wasserstoff-Elektronen oder Sauerstoff-Elektronen - und sie ist außerdem so klein, dass dadurch bedingte Effekte vernachlässigt werden können.
Elektronen sind von einem elektrischen Feld umgeben und bei einer Beschleunigung tritt eine gegenseitige Behinderung auf. Je mehr Elektronen sich gleichzeitig in Bewegung setzen oder ihre Driftgeschwindigkeit ändern und je näher sie sich sind, um so mehr behindern sie sich. Es handelt sich hier um einen grundlegenden, rein elektrischen Effekt, der mit mechanischen Vorstellungen nicht zu erklären ist. Für ein weitergehendes Studium muß auf Lehrbücher mit den entsprechenden Kapiteln zum Thema "Elektromagnetische Induktion" verwiesen werden.
Für die weiteren Ausführungen reicht es aus zu wissen, dass es auf einer Doppelleitung eine Art Trägheit der Elektronen gibt, die sich immer dann bemerkbar macht, wenn die Driftgeschwindigkeit der Elektronen geändert werden soll, das heißt, wenn sich die Stromstärke ändert.
Diese trägheitsartigen Eigenschaft einer Doppelleitung nennt man Induktivität und kennzeichnet sie mit L. Wie bei der Kapazität läßt sich L ebenfalls durch die Änderung des Abstandes der Leitungen beeinflussen sowie durch Einbringen von Materialien mit speziellen magnetischen Eigenschaften.
Nähere Erläuterungen zu diesen Auswirkungen siehe unter: Abstandsänderung und Auswirkung eines Dielektrikums
Ein physikalisches Verständnis dieser Effekte ist nicht mit kurzen Erklärungen zu erreichen, sondern setzt gründliche Kenntnisse zum Thema "Elektromagnetische Induktion" voraus.
2.3.4. Mathematische Beziehung zwischen Z, L und C
Qualitative Beschreibung
Wird die Induktivität L einer Doppelleitung vergrößert, so wird bei vorgegebener Spannung wegen der verstärkten gegenseitigen Behinderung der Elektronen ein kleinerer Strom fließen. Somit gilt: Je größer bzw. kleiner die Induktivität einer Doppelleitung, desto größer bzw. kleiner ist die Impedanz Z= U/I .
Wird die Kapazität einer Doppelleitung vergrößert, so sind zusätzliche Elektronen erforderlich, um eine vorgegebene Spannung aufrecht zu erhalten. Damit wird der Strom im Verhältnis zur Spannung vergrößert und es gilt: Je größer bzw. kleiner die Kapazität einer Doppelleitung, desto kleiner bzw. größer ist die Impedanz Z= U/I .
Quantitavite Beschreibung
Aus der Theorie abgeleitet und experimentell bestätigt ergibt sich für die Impedanz einer Wellenleitung die folgende Beziehung: Z = √L/C.
Wird L in Henry gemessen und C in Farad, so erhält man für Z die Einheit Ohm.
Für den Wellenwiderstand Z einer Doppelleitung ist es somit ohne Bedeutung, ob beispielsweise die Kapazität verdoppelt oder die Induktivität halbiert wird. Die Auswirkungen auf den Wellenwiderstand sind gleich. Der Wellenwiderstand bleibt auch unverändert, wenn sowohl die Kapazität als auch die Induktivität um den gleichen Faktor verändert werden.
Sowohl L als auch C hängen vom Abstand der beiden Leitungen ab. Sollen also L und C unabhängig voneinander geändert werden, so ist dies nur durch das Einbringen entsprechender Materialien möglich (Dielektrikum zur Änderung von C, magnetische Materialien zur Änderung von L)
2.3.5. Doppelleitung mit veränderbaren Werten für die Kapazität
Das Simulationsprogramm TL bietet die Möglichkeit, den Wert der Kapazität C für die gesamte Leitung zu verändern und zwar ohne Änderung von L. Experimentell wird dies durch das Einbringen unterschiedlicher Dielektrika erreicht.
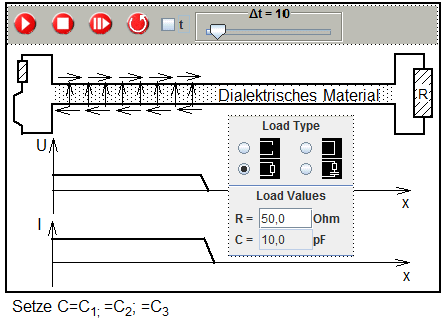
Wellenfront auf einer Doppelleitung mit variabler Kapazität
(vorbereitete Simulation: 2-3-5-Leitung-mit-Z=40 Ohm.xml)
Nach Start der Simulation läuft eine Wellenfront über die Leitung, bei der das Verhältnis Z = U/I mit der Größe von C variiert. Den zu der jeweiligen Kapazität zugehörige Wert für Z erhält man durch Bestimmung des Abschlußwiderstandes R, bei dem keine Reflexion auftritt. Der Wert für R kann in dem geöffneten Eingabefenster variiert werden.
2.3.6. Doppelleitung mit veränderbaren Werten für die Induktivität
Das Simulationsprogramm TL bietet die Möglichkeit, den Wert für die Induktivität L bei konstantem C längs der gesamten Leitung zu verändern. Experimentell wird dies durch das Einbringen unterschiedlicher magnetischer Materialien erreicht.
Wellenfront auf einer Doppelleitung mit variabler Induktivität
(vorbereitete Simulation: 2-3-6-Leitung-mit-Z=90 Ohm.xml)
Nach Start der Simulation läuft eine Wellenfront über die Leitung, bei der das Verhältnis Z = U/I mit der Größe von L variiert. Den zu der jeweiligen Induktivität zugehörige Wert für Z erhält man durch Bestimmung des Abschlußwiderstandes R, bei dem keine Reflexion auftritt. Der Wert für R kann in dem geöffneten Eingabefenster variiert werden.
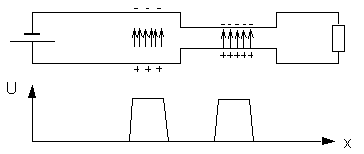
Kapazität als Funktion des Abstandes
Durch Änderung des Abstands der beiden Leitungen einer Doppelleitung wird die Coulombkraft zwischen den unterschiedlich gepolten Oberflächenladungen verändert. Je kleiner der Abstand, desto mehr ziehen sich die Ladungsträger an und je größer ist die Dichte der Ladungsträger, die sich beim Anlegen einer bestimmten Spannung einstellt und umgekehrt.
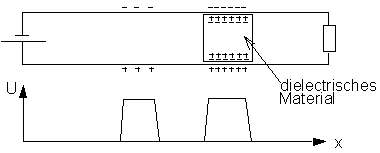
Kapazität und Dielektrikum
Isolatoren sind Materialien, deren Elektronen sich nicht frei bewegen können, sondern fest an den Atomen bzw. Molekülen des Festkörpers gebunden sind. Allerdings können sich diese Elektronen und die positiven Gitterteilchen unter dem Einfluß eines äußeren elektrischen Feldes etwas gegeneinander verschieben, so daß jedes Gitterteilchen einen kleinen elektrische Dipol bildet. Diese Materialeigenschaft nennt man "dielektrisch" und das Material selbst "Dielektrikum".
Befindet sich ein solches Dielektrikum zwischen einer Doppelleitung, und befinden sich auf dieser Doppelleitung Oberflächenladungen, so bilden sich in diesem Dielektrikum elektrische Dipole aus. Diese sind derart gerichtet, daß den negativen Oberflächenladungen eine positiv geladenen Oberfläche gegenübersteht und umgekehrt.
Induktivität als Funktion der Entfernung
Elektronen behindern sich gegenseitig sobald sie beschleunigt werden. Je mehr Elektronen ihre Geschwindigkeit ändern und je geringer ihr gegenseitiger Abstand, um so mehr behindern sie sich.
Hieraus folgt, dass die Induktivität von dem Abstand zwischen den Leitungen einer Doppelleitung abhängig ist. Je größer der Abstand, desto kleiner die Induktivität
Induktivität und magnetische Materialien
Die gegenseitige Behinderung von beschleunigten Elektronen - die Induktivität - wird durch magnetischews Material verstärkt, dass sich im Raum zwischen den Leitungen einer Doppelleitung befindet. Mit Hilfe solcher Materialien ist es daher möglich, die Induktivität einer Doppelleitung bei gleichbleibender Kapazität zu ändern.
Dieser Effekt kann nicht in Analogie zu mechanischen Vorgängen erklärt werden. Es handelt sich hier um ein Grundphänomen der elektromagnetischen Induktion und wird in allen diesbezüglichen Lehrbüchern ausführlich behandelt.
zurück zur Starseite
Für den Wellenwiderstand Z einer Doppelleitung ist es somit ohne Bedeutung, ob beispielsweise die Kapazität verdoppelt oder die Induktivität halbiert wird. Die Auswirkungen auf den Wellenwiderstand sind gleich. Der Wellenwiderstand bleibt auch unverändert, wenn sowohl die Kapazität als auch die Induktivität um den gleichen Faktor verändert werden.
Sowohl L als auch C hängen vom Abstand der beiden Leitungen ab. Sollen also L und C unabhängig voneinander geändert werden, so ist dies nur durch das Einbringen entsprechender Materialien möglich (Dielektrikum zur Änderung von C, magnetische Materialien zur Änderung von L)
Wellenfront auf einer Doppelleitung mit variabler Kapazität
(vorbereitete Simulation: 2-3-5-Leitung-mit-Z=40 Ohm.xml)
Wellenfront auf einer Doppelleitung mit variabler Induktivität
(vorbereitete Simulation: 2-3-6-Leitung-mit-Z=90 Ohm.xml)
Kapazität als Funktion des Abstandes
Durch Änderung des Abstands der beiden Leitungen einer Doppelleitung wird die Coulombkraft zwischen den unterschiedlich gepolten Oberflächenladungen verändert. Je kleiner der Abstand, desto mehr ziehen sich die Ladungsträger an und je größer ist die Dichte der Ladungsträger, die sich beim Anlegen einer bestimmten Spannung einstellt und umgekehrt.
Kapazität und Dielektrikum
Isolatoren sind Materialien, deren Elektronen sich nicht frei bewegen können, sondern fest an den Atomen bzw. Molekülen des Festkörpers gebunden sind. Allerdings können sich diese Elektronen und die positiven Gitterteilchen unter dem Einfluß eines äußeren elektrischen Feldes etwas gegeneinander verschieben, so daß jedes Gitterteilchen einen kleinen elektrische Dipol bildet. Diese Materialeigenschaft nennt man "dielektrisch" und das Material selbst "Dielektrikum".
Befindet sich ein solches Dielektrikum zwischen einer Doppelleitung, und befinden sich auf dieser Doppelleitung Oberflächenladungen, so bilden sich in diesem Dielektrikum elektrische Dipole aus. Diese sind derart gerichtet, daß den negativen Oberflächenladungen eine positiv geladenen Oberfläche gegenübersteht und umgekehrt.
Die Wechselwirkung zwischen den Dipolen und den Oberflächenladungen ist wegen des geringeren Abstandes deutlich größer als die Interaktion der Oberflächenladungen ohne Dielektrikum. Im Endergebnis erzielt man den gleichen Effekt, wie bei einer Veringerung des Abstandes zwischen den Leitungen: die Dichte der Oberflächenladungen wird bei gleicher Spannung erhöht und somit die Kapazität.
Induktivität als Funktion der Entfernung
Elektronen behindern sich gegenseitig sobald sie beschleunigt werden. Je mehr Elektronen ihre Geschwindigkeit ändern und je geringer ihr gegenseitiger Abstand, um so mehr behindern sie sich.
Hieraus folgt, dass die Induktivität von dem Abstand zwischen den Leitungen einer Doppelleitung abhängig ist. Je größer der Abstand, desto kleiner die Induktivität
Induktivität und magnetische Materialien
Die gegenseitige Behinderung von beschleunigten Elektronen - die Induktivität - wird durch magnetischews Material verstärkt, dass sich im Raum zwischen den Leitungen einer Doppelleitung befindet. Mit Hilfe solcher Materialien ist es daher möglich, die Induktivität einer Doppelleitung bei gleichbleibender Kapazität zu ändern.
Dieser Effekt kann nicht in Analogie zu mechanischen Vorgängen erklärt werden. Es handelt sich hier um ein Grundphänomen der elektromagnetischen Induktion und wird in allen diesbezüglichen Lehrbüchern ausführlich behandelt.
zurück zur Starseite