2.2.1. Reflexion an einer offenen Doppelleitung (R = ∞)

In Analogie zu einem mechanischen System kann man bei einer elektrischen Doppelleitung eine Reflexion erwarten, wenn ein Puls oder eine Wellenfront auf einen Abschlußwiderstand trifft.
Sind die beiden Leitung an ihren Enden unterbrochen, so entspricht dies einem Abschlußwiderstand R = ∞
Die folgende Abbildung zeigt eine solche Doppelleitung mit einem Puls kurz vor dem Auftreffen und im Augenblick der Reflexion.

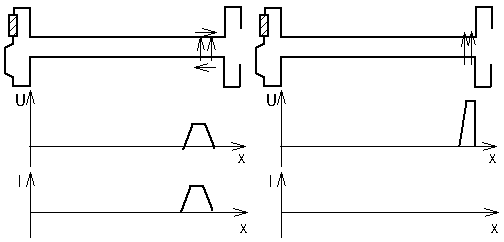
Links: Ein Puls kurz vor dem Auftreffen auf eine Unterbrechung (R = ∞Ω)
Rechts: Strom/Spannungsverhältnisse im Augenblick der Reflexion

Bedingt durch die Unterbrechung der Leitungen wird der Strom gestoppt, während sich die Spannung erhöht. Ist dem Augenblick, in dem die Stromstärke auf Null gesunken ist, erreicht die Spannung ein Maximum.
Wie in dem Kapitel "2.2.4. Ausbreitung eines Spannungspulses auf einer Doppelleitung" gezeigt wurde, breitet sich ein solcher Spannungspuls nach beiden Seiten hin aus.
Die Ausbreitung nach rechts ist jedoch wegen der Leitungsunterbrechung nicht möglich. Dieser Anteil wird deshalb ebenfalls nach links reflektiert und mit der nach links sich ausbreitenden Hälfte überlagert. Als Ergebnis ergibt sich eine Reflexion des ursprünglichen Pulses ohne Änderung der Form.
Mit Hilfe der Simulation kann dieser Vorgang im einzelnen verfolgt werden.

(vorbereitete Simulation: 2-2-1-Puls-R-unendlich.xml)

2.2.2. Reflexion an einem Kurzschluß als Abschlußwiderstand

Sind die beiden Enden einer Doppelleitung kurzgeschlossen, so entspricht dies einem Abschlußwiderstand von 0 Ω.
Die folgende Abbildung zeigt eine solche Doppelleitung mit einem Puls kurz vor dem Auftreffen und im Augenblick der Reflexion.

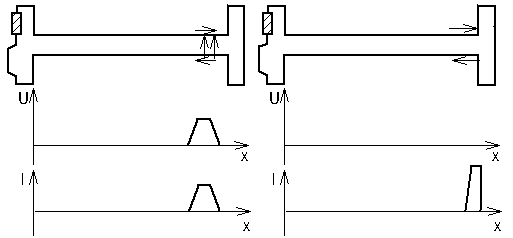
Links: Ein Puls kurz vor dem Auftreffen auf einen Kurzschluß (R=0 Ω)
Rechts: Strom/Spannungsverhältnisse im Augenblick der Reflexion

An der Verbindungsstelle beider Leitungen nähern sich die unterschiedlich gepolten Oberflächenladungen auf den beiden Leitungen gegenseitig an und neutralisieren sich. Während der Annäherung vergrößert sich ihre gegenseitige Coulomb-Wechselwirkung mit dem Ergebnis einer beschleunigenden Wirkung auf die driftenden Elektronen.
Sind alle Oberfächenladungen neutralisiert, so existiert an der Kurzschlußstelle eine Zone driftender Elektronen ohne Spannung zwischen den Leitern.
Diese Situation und der dann einsetzende Vorgang entspricht dem Sachverhalt, der in dem Kapitel "2.2.5. Ausbreitung eines Zone mit driftenden Elektronen auf einer Doppelleitung" dargestellt wurde.

Eine solche Zone breitet sich normaler Weise nach beiden Seiten hin aus. Am Ende einer kurzgeschlossenen Doppelleitung bedeutet dies jedoch, dass die beiden Pulshälften auf den getrennt Leitungen zurücklaufen.
Mit Hilfe der Simulation kann dieser Vorgang im einzelnen verfolgt werden.

(vorbereitete Simulation: 2-2-2-Puls-R-null.xml)

2.2.3. Reflexionsfreier Abschluß einer Doppelleitung

Im Fall einer mechanischen Doppelleitung gibt es den Fall, dass der Abschlußwiderstand das Verhältnis ΔP/I beim Auftreffen eines Pulses nicht verändert. Unter dieser Bedingung tritt keine Reflexion auf.
Es liegt nahe anzunehmen, dass ein solcher reflexionsfreier Abschluß auch bei einer elektrischen Doppelleitung auftritt, bei der der Abschlußwiderstand das Verhältnis U/I nicht verändert.
Die Simulation bietet die Möglichkeit, die Reflexion für unterschiedliche Widerstandwerte zu verfolgen und festzustellen, bei welchem Wert keine Reflexion auftritt.

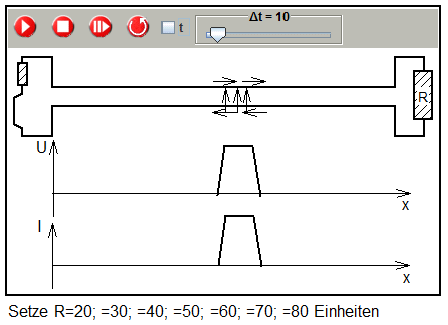
Simulation der Reflexion eines Pulses auf einer Doppelleitung
mit verschiedenen Abschlußwiderständen
(vorbereitete Simulation: 2-2-3-Puls-R-50Ohm.xml)

Das Verhältnis U/I, das notwendig ist, damit eine lineare Pulsübertragung möglich ist, wird durch eine besondere Eigenschaft der entsprechenden Doppelleitung bestimmt, die als "Wellenwiderstand" oder "Impedanz" (abgekürzt Z) bezeichnet wird. Die Einheit, in der Z gemessen wird, ist Ohm (Ω).

Das Verhältnis U/I entspricht dem Wert eines Widerstandes und bestimmt, bei welcher Spannung welcher Strom durch den Widerstand fließt.
Somit liegt es nahe zu vermuten, dass ein reflexionsfreier Abschluß gegeben ist, wenn bei einer Doppelleitung mit dem Wellenwiderstand Z₁ und einem Abschlußwiderstand R₁ die Bedingung gilt: Z₁ = R₁. Theorie und Simulation bestätigen diese Vermutung.

In allen anderen Fällen (R>Z or R<Z)tritt eine partielle Reflexion auf.
Es ist sicherlich lehrreich, diese Fälle in der gleichen Weise zu analysieren, wie dies für R=0 and R = ∞ Ω durchgeführt wurde.

zurück zur Starseite