Fachdidaktik Physik
vom Feinsten

Axoren als Dreifaktorenprodukte.
Addieren von Axoren.
Namen und Symbole für Axoren und Vektoren

Gibt es eine negative Geschwindigkeit?
Darf man Gleichungen, wie v_G= +3m/s oder v_G=-3m/s, lesen als 2-Faktoren-Produkte, bestehend jeweils aus einer Bezugsgröße und einem Ausmaßfaktor mit einem positiven oder negativen Zahlenwert?
Weninger widerspricht und begründet ausführlich, warum die obigen Gleichungen als 3-Faktoren-Produkte zu behandeln sind, in der Sprache Weninges als Axoren. Sie bestehen jeweils aus einem Orientierungsfaktor (+1) oder (-1), einem Ausmaßfaktor und einer Bezugsgröße. Die obigen Gleichungen sind wie folgt zu schreiben: v_G= (+1) • 3 • m/s oder v_G = (-1) • 3 • m/s.

Für eine Axor-Größe wird ein eigenes Symbol eingeführt, das bisher den Vektoren vorbehalten war; Beispiel: 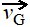. Vektoren kennzeichnet Weninger mit einem hochgestellten Zweibein, Beispiel: . Diese Formelzeichen gelten zunächst nur für die vorliegende Arbeit, um die Erarbeitung einer grundsätzlichen Klarheit zu unterstützen. Zuständige Gremien können später entscheiden, ob diese Zeichen allgemein übernommen werden.

Die Zusammenfassung dieser Orientierungsfaktoren mit den mathematischen Zeichen "+" und "-" ergibt ein rein mathematischen Produkt, mit dem elegant zu rechnen ist, daß aber ohne hinreichende Erklärung unverständlich bleibt. Eine Geschwindigkeit kann beständig kleiner werden, bis sie gleich null ist. Schüler können sich aber nicht vorstellen, dass die Geschwindigkeit als solche kleiner als null und doch wohl erst damit negativ (< 0) werden kann.

Lesen Sie selbst:
Abschnitt 4