zurück zur Startseite

Kondensatoreigenschaften elektrischer Schaltungen

5.1. Eigenschaften eines Kondensators

Ein Kondensator besteht im Prinzip aus zwei relativ großen metallischen Folien -oder Isolatorschichten mit metallischer Oberfläche - die durch eine m&ouuml;glichst d&uuuml;nnen Schicht getrennt sind. Diese Trennschicht ist in der Regel mit einem isolierenden Material gef&uuuml;llt, so daß keine leitende Verbindung zwischen den beiden Metallflächen besteht.

Abb 14: Prinzip eines Kondensators mit angeschlossener Spannungsquelle
Deutlich erhöhte Ladungsdichte zwischen den Platten
im Vergleich zu der Ladungsdichte auf den Leitungen

Wird eine Spannungsquelle &uuuml;ber zwei Leitungen mit einem Kondensator verbunden, so werden durch die Kraft der Spannungsquelle Elektronen auf eine der beiden Kondensatorhälften aufgebracht, während sich auf der anderen Kondensatorhälfte die dann fehlenden Elektronen als positive Ladungen bemerkbar machen.
Wegen der geringen Dicke der Trennschicht tritt nun die anziehende Wechselwirkung zwischen diesen unterschiedlich gepolten Ladungen auf den inneren Oberflächen des Kondensators in Erscheinung mit dem Ergebnis, daß dadurch die gegenseitige Abstoßung zwischen den gleichpoligen Ladungen verringert wird.
Das bedeutet, daß die Kraft der Spannungsquelle eine viel gr&ouuml;ßere Dichte von Elektronen und entsprechenden positiven Ladungen innerhalb des Kondensators hervorrufen kann, bevor wieder ein Gleichgewicht mit den abstoßenden Kräften zwischen den gleichpoligen Ladungen und der Kraft der Spannungsquelle erreicht wird.
Je d&uuuml;nner die isolierende Trennschicht, desto stärker ist die gegenseitige Anziehung der Ladungen &uuuml;ber diese Trennschicht hinweg, um so mehr wird die gegenseitige Abstoßung gleichpoliger Ladungen auf jeder Seite neutralisiert und desto gr&ouuml;ßer ist die Dichte der Ladungen, die sich beim Anlegen einer bestimmten Spannung im Kondensator einstellt.
Bei einem normalen Leiter ist die Zahl der zusätzlichen Ladungen auf der Oberfläche sehr gering, da die Abstoßungskräfte zwischen den Ladungen sehr groß sind und sich schon bei einer relativ geringen Dichte ein Gleichgewicht mit der antreibenden Kraft der Spannungsquelle einstellt. Die Elektronen auf der Oberfläche von Leiter sind also - alltagssprachlich ausgedr&uuuml;ckt - sehr wenig elastisch und lassen sich nur sehr wenig zusammendr&uuuml;cken. Dagegen k&ouuml;nnen Ladungen auf der Innenseite eines Kondensators wegen der gegenseitigen Anziehung &uuuml;ber die Trennlinie hinweg sehr viel mehr zusammengedr&uuuml;ckt werden, sie sind also sehr viel elastischer als bei einem normalen Leiter.

5.2. Kapazität eines Kondensators

Die Größe der Ladung q, die sich durch eine angelegte Spannung in einen Kondensator hineindr&uuuml;cken läßt bis ein Gleichgewichtszustand eintritt, ist proportional zu der angelegten Spannung U. In anderen Worten: Q/U ist eine für jeden Kondensator charakteristische Konstante. Sie wird Kapazität genannt und mit C gekennzeichnet. C = Q/U.
Die Einheit der Kapazität ist das Farad, abgek&uuuml;rzt F, zu Ehren des englischen Physikers Michael Faraday (1791-1867).
Die Kapazität 1 F bedeutet, daß beim Anlegen einer Spannung von 1 Volt die Einheitsladung 1 Q = 6, 2 10¹⁸ Elektronen in einen Kondensator hineinfließen, bis ein Gleichgewichtszustand erreicht wird. Dies ist ein sehr großer Wert, der mit technischen Mitteln in aller Regel nicht erreicht wird. Die in der Technik &uuuml;blichen Kapazitäten liegen im Bereich von mμF bis nF (10-6 bis 10-9F).

5.2. Laden und Entladen von Kondensatoren

Wird eine Spannungsquelle &uuuml;ber zwei Leitungen mit einem Kondensator verbunden, so erscheint es plausibel, daß ein stationärer Zustand nicht augenblicklich erreicht wird. Es m&uuuml;ssen durch den Widerstand der Leitungen eine große Anzahl von Elektronen auf die Innenseite des Kondensators gebracht werden bis die dort erreichte Dichte so groß ist, daß durch die auftretenden Abstoßungskräfte ein weiterer Elektronenzufluß verhindert wird.
Es erscheint weiterhin plausibel, daß die Zeitdauer bis zum Erreichen eines stationären Zustandes um so länger ist, je gr&ouuml;ßer die Kapazität und je gr&ouuml;ßer der Widerstand in den Zuleitungen ist.
Die Stärke des Ladungsstromes ist dabei nicht konstant. Der Strom nimmt mit der Ladungszeit ab, da mit zunehmender Aufladung des Kondensators die der Spannung entgegenwirkenden Coulombkräfte zunehmen.
Die Theorie ergibt, daß der zeitliche Verlauf des Ladungsstromes einer e-Funktion folgt.

Abb 15: Ladestrom eines Kondensators in Abhängigkeit von der Ladezeit

5.3. Einfache Schaltungen eines elektrischen Stromkreises mit und ohne Leitungskapazitäten

Üblicherweise gilt als einfachste Schaltung eines elektrischen Stromkreises die Verbindung einer Spannungsquelle &uuuml;ber zwei Leitungen mit einem Widerstand.

Abb 16: Schaltbild eines einfachen Stromkreises

Dies ist eine idealisierte Darstellung, denn sie ber&uuuml;cksichtigt nicht die Tatsache, daß die Oberflächen der Leitungen eine Art Kondensator darstellen, der eine zwar kleine, aber stets von Null verschiedene Kapazität besitzt.
Sofern nur stationäre Zustände betrachtet werden, ohne die Frage nach den Ursache f&uuuml;r solche Zustände zu stellen, gen&uuuml;gt diese Art der Darstellung.

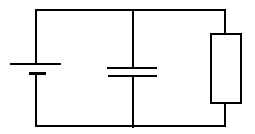
Abb 17: Ersatzschaltbild eines einfachen Stromkreises unter Berücksichtigung des Kapazität der Leitungen

Eine genauere Betrachtung aber verlangt, die Oberflächen der Leitungen als eine kleine, stets vorhandene Kapazität zu ber&uuuml;cksichtigen.
Dies bedingt u.a., daß je nach Gr&ouuml;ße dieser Kapazität der &uuuml;bergangsprozeß von einem stationären Zustand zum nächsten mehr oder weniger verz&ouuml;gert wird.
In aller Regel ist diese Verz&ouuml;gerung sehr klein und nur durch eine aufwendige Versuchsanordnung festustellen. F&uuuml;r praktische Arbeiten im Unterricht kann diese Verz&ouuml;gerung vernachlässigt werden. Die Frage ist. ob das explizite Behandeln diese Verz&ouuml;gerungen nicht zu einem umfassenderen und tieferen Verständnis der jeweils im Stromkreis ablaufenden Prozesse f&uuuml;hrt. Solange nur ein Wissen auf der Basis des Ohmschen Gesetzes und der Kirchhoffschen Regeln vermittelt wird. bleibt im Verständnius der Sch&uuuml;ler der Stromkreis ein System, welches bei änderungen bestimmter Parameter spontan von einen Gleichgewichtsustand in einen anderen springt. Gr&uuuml;nden f&uuuml;r die Art und den Ablauf solcher Veränderungen gehen verloren.
In einem gesonderten Kapitel wird gezeigt, wie mit Hilfe speziellen Simulationsprogramme eine Behandlung der real ablaufenden &uuuml;bergangsprozesse in Stromkreises im Untgerricht unterst&uuuml;tzt werden kann.

zurück zur Startseite