zurück zur Startseite
Spannung und Energieumsatz
3.1.Quantitative Bestimmung der Spannung
In der Physik ist es nun erforderlich, daß eine Gr&oum;ße wie die Spannung nicht nur qualitativ erklärbar, sondern auch quantitativ bestimmbar ist. Um eine solche quantitative Bestimmung durchf&uum;hren zu k&oum;nnen, ist es nicht m&oum;glich, die Oberflächenladungen bzw. die dadurch hervorgerufenen Coulombkräfte direkt zu messen. Die Dichte der zusätzlichen Elektronen und der Gradient ihrer Dichteverteilung sind i.a. sehr klein und außerdem von vielen äußeren, geometrischen Faktoren abhängig. Unabhängig von äußeren Faktoren ist dagegen die Arbeit, die von diesen Kräften verrichtet wird und damit der Energieumsatz, der bei einem bestimmten Stromfluß und einer bestimmten Spannung auftritt.
Damit ist die M&oum;glichkeit gegeben, die Spannung zwischen zwei Punkten A und B quantitativ zu beziehen auf diejenige Energie, die umgesetzt wird, wenn eine bestimmte Ladung q von A nach B transportiert wird. In mathematischer Form:
U = E/q.
Numerisch stimmt die Gr&oum;ße einer Spannung &uum;berein mit der Energie, die beim Transport einer Einheitsladung Q umgesetzt wird.
Die Einheit der Spannung ist 1 Volt, abgek&uum;rzt V, zu Ehren des italienischen Physikers Alessandro Graf von Volta (1745-1827).
3.2. Energieumsatz in Abhängigkeit von Spannung und Stromstärke
IGegeben sei ein elektrischer Strom der Stärke I = q/t bei einer zwischen den Punkten A und B angelegten Spannung U = E/q.
Fließt ein elektrischen Strom längs der Strecke von A nach B während der Zeitdauer t, so wird dabei die Ladung q = I*t von A nach B transport
.
F&uum;r den Energieumsatz E folgt:
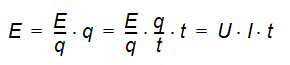
3.3. Erweiterte Spannungsdefinition zwischen zwei Punkten im Raum
Die Einf&uum;hrung der Spannung als E/q macht es m&oum;glich, eine Spannung nicht nur bei vorhandener Ladungstrennung sondern auch zwischen zwei Punkten A und B im Raum zu definieren, die sich zwischen getrennten Ladungen befinden, selbst aber keine unterschiedlichen Ladungen aufweisen.

Abb 7.: Spannung zwischen zwei ungeladenen Punkten
In aller Regel werden A und B einen unterschiedlichen Abstand zu den äußeren Ladungen aufweisen und somit wird ein Ladungstransport zwischen A und B mit einer Energieumwandlung verbunden sein.
Auf der Grundlage der obigen Definition U = E/q kann zwischen den Punkten A und B eine Spannung definiert werden, auch wenn an den beiden Orten keine getrennten Ladungen vorhanden sind.
Die beiden Orte A und B unterscheiden sich dann nicht durch unterschiedliche Ladungsdichten, sondern durch unterschiedliche Abstände innerhalb eines Systems getrennter Ladungen.
zurück zur Startseite
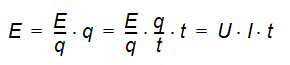
3.3. Erweiterte Spannungsdefinition zwischen zwei Punkten im Raum
Die Einf&uum;hrung der Spannung als E/q macht es m&oum;glich, eine Spannung nicht nur bei vorhandener Ladungstrennung sondern auch zwischen zwei Punkten A und B im Raum zu definieren, die sich zwischen getrennten Ladungen befinden, selbst aber keine unterschiedlichen Ladungen aufweisen.

Abb 7.: Spannung zwischen zwei ungeladenen Punkten
In aller Regel werden A und B einen unterschiedlichen Abstand zu den äußeren Ladungen aufweisen und somit wird ein Ladungstransport zwischen A und B mit einer Energieumwandlung verbunden sein.
Auf der Grundlage der obigen Definition U = E/q kann zwischen den Punkten A und B eine Spannung definiert werden, auch wenn an den beiden Orten keine getrennten Ladungen vorhanden sind.
Die beiden Orte A und B unterscheiden sich dann nicht durch unterschiedliche Ladungsdichten, sondern durch unterschiedliche Abstände innerhalb eines Systems getrennter Ladungen.

Abb 7.: Spannung zwischen zwei ungeladenen Punkten
zurück zur Startseite