zurück zur Startseite
Oberflächenladungen in Stromkreisen
2.1. Oberflächenladungen auf Leitungen
Werden die Kontakte der Spannungsquelle mit metallischen Leitern verbunden, so ist dies gleichbedeutend mit einer Vergr$ouml;ßerung der Oberfläche dieser Kontakte.
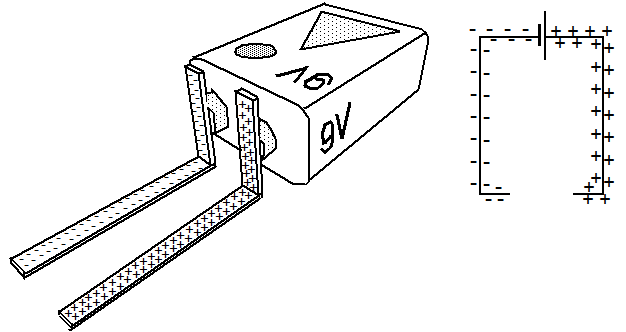
Abb.1. Spannungsquelle mit angeschlossenen Leitern und Oberflächenladungen
Auf Grund der gegenseitigen Abstoßung zwischen den Ladungsträgern verteilen sich die Oberflächenladungen auf diese vergr$ouml;ßerte Oberfläche, wobei sich ihre Dichte verringert. Damit wird f$uuml;r einen kurzen Augenblick das Gleichgewicht zwischen der Kraft der Spannungsquelle und den Coulombkräfte zu Gunsten der ersteren aufgehoben. Es fließen zusätzliche Elektronen auf die vergr$ouml;ßerte Oberfläche, bis wieder die f$uuml;r die Spannungsquelle charakteristische Dichte erreicht und damit das Gleichgewicht der Kräfte wieder hergestellt ist.

Abb.1. Spannungsquelle mit angeschlossenen Leitern und Oberflächenladungen
2.2. Oberflächenladungen im geschlossenen Stromkreis
Werden nun die Enden der Leitungen $uuml;ber einen Widerstand verbunden, und ist die Spannungsquelle in der Lage, die abfließenden Elektronen nachzuliefern, so werden die gesamten freien Elektronen im Innern der Leitern langsam im Kreis herumfließen.
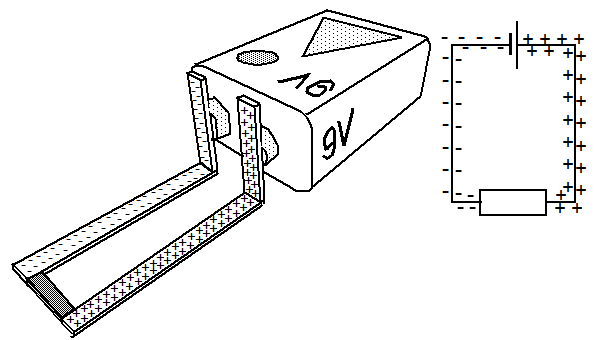
Abb 2.: Geschlossener Stromkreis mit Oberflächenladungen auf den Leitern
Sofern die antreibende Kraft der Spannungsquelle durch den Stromfluß nicht nachläßt, werden sich weiterhin zusätzliche Ladungen auf den Oberflächen der Leitungen befinden, die nun an der Fließbewegung der Elektronen im Innern teilnehmen.

Abb 2.: Geschlossener Stromkreis mit Oberflächenladungen auf den Leitern
2.3.Oberflächenladungen bei stromdurchflossenen Leitern
Fließt durch einen homogenen Leiter ein konstanter elektrischer Strom, so muß, da jeder Leiter einen bestimmten Widerstand aufweist, im Innern des Leiter eine konstante Kraft vorhanden sein, die die Driftbewegung der Elektronen trotz des bremsenden Widerstandes aufrecht erhält.
Eine solche konstante und stets axial ausgerichtet Kraft wird erzeugt durch eine bestimmte Verteilung von Oberflächenladungen auf den betreffenden Leitern.

Abb 3.: Lineare Dichteverteilung von Oberflächenladungen bei einem geraden Leiterabschnitt
Betrachtet man als einfachsten Fall einen geradlinigen, homogenen Leiter, so kann man auf der Grundlage des Coulombschen Kraftgesetzes berechnen, daß eine gleichmäßige, d.h. linear abnehmende Dichteverteilung von Oberflächenladungen die erforderliche konstante Kraft im Innern des Leiters bewirkt. Man spricht auch von einem linearen Gradienten der Dichteverteilung, der im Innern eine konstante Kraft bewirkt. Dies gilt um so genauer, je länger und dünner der Leiter ist.
Bei kurzen bzw. gekrümmten Leitern ergeben sich komplizierte Dichteverteilungen, um im Innern der Leiter eine konstante, axial gerichtete Antriebskraft zu erzeugen. Die entsprechenden Berechnungen sind jedoch aufwendig. Allgemein läßt sich voraussagen, daß die Dichte der Elektronen auf der Oberfläche einer Außenkrümmung größer sein muß als auf der Innenseite und umgekehrt für positive geladene Oberflächen.

Abb 4: Verteilung von Oberflächenladungen bei gekr$uuml;mmten Leitern (qualitativ)
Da der Widerstand in metallischen Leitern sehr gering ist, sind die Gradienten der Dichteverteilung der Oberflächenladungen äußerst gering und k$ouml;nnen in aller Regel vernachlässigt werden. F$uuml;r ein qualitatives Verständnis sind aber die Existenz von Oberflächenladungen und die Gradienten der Dichteverteilung unerläßlich.
2.4.Ladungsschichten an den Grenzen zwischen
Widerstand und Leiter
Wird ein metallischer Leiter mit einem Widerstand verbunden, so ergibt sich quer durch den Leiter eine Schicht, die das Gebiet hoher Leitfähigkeit von dem Widerstand mit geringer Leitfähigkeit trennt.

Abb 5: Geladene Trennschichten zwischen Widerstand und Leiter
Je nach Art des Widerstandes besitzt diese Trennschicht eine unterschiedliche Dicke in der sich die Leitfähigkeit des Materials kontinuierlich oder mehr oder weniger sprunghaft ändert.
Diese Trennschicht vor und hinter einem Widerstand bleibt nicht neutral, wenn Elektronen durch den Widerstand getrieben werden. In der Trennschicht vor dem Widerstand (bezogen auf die Fließrichtung der Elektronen) stauen sich ein paar Elektronen, da vor ihnen ein Gebiet mit abnehmender Leitfähigkeit liegt. Diese Trennschicht wird also negativ geladen. Aus der Trennschicht hinter dem Widerstand entfernen sich ein paar Elektronen, da sich vor ihnen ein Gebiet mit gr$ouml;ßerer Leitfähigkeit befindet. In dieser Trennschicht bleiben Atomr$uuml;mpfe zur$uuml;ck, denen ein Elektron fehlt. Diese Trennschicht wird somit positiv aufgeladen.
Sowohl die unterschiedlich verteilten Ladungsträger auf den Oberflächen als auch die in den Trennschichten erzeugen abstoßende bzw. anziehende Kräfte, die die frei beweglichen Elektronen des Metalls durch den Widerstand treiben. Wird nun die Kraft an der Batterie erh$ouml;ht, so erh$ouml;ht sich der Gradient der Dichteverteilung der Oberflächenladungen, und es treten mehr unterschiedlich gepolte Ladungen vor und hinter dem Widerstand auf. Dadurch erh$ouml;ht sich die Kraft auf die beweglichen Ladungen innerhalb des Widerstandes und somit die Stromstärke, d.h. die Zahl der Ladungsträger, die pro Zeiteinheit durch einen Leiterquerschnitt fließen.
2.5.Spannung und Oberflächenladungen
Eine Spannung zwischen zwei Punkten innerhalb eines Stromkreises tritt immer dann auf, wenn eine Ladungstrennung vorliegt, wenn also auf den Oberflächen von zwei unterschiedlichen Leiterteilen unterschiedlich gepolte Ladungsträger vorhanden sind oder die Dichte der Oberflächenladung verschieden ist. Die dann auftretenden Coulombkräfte streben einen Ausgleich an und sind somit der Grund f$uuml;r die auftretende Spannung. Dies gilt sowohl f$uuml;r elektrostatische Anordnungen als auch f$uuml;r Spannungen an einem stromdurchflossenen Widerstand.
Spannung wird im deutschen Sprachraum mit U gekennzeichnet im angel-sächsischen mit V.
zurück zur Startseite

Abb 3.: Lineare Dichteverteilung von Oberflächenladungen bei einem geraden Leiterabschnitt
Bei kurzen bzw. gekrümmten Leitern ergeben sich komplizierte Dichteverteilungen, um im Innern der Leiter eine konstante, axial gerichtete Antriebskraft zu erzeugen. Die entsprechenden Berechnungen sind jedoch aufwendig. Allgemein läßt sich voraussagen, daß die Dichte der Elektronen auf der Oberfläche einer Außenkrümmung größer sein muß als auf der Innenseite und umgekehrt für positive geladene Oberflächen.

Abb 4: Verteilung von Oberflächenladungen bei gekr$uuml;mmten Leitern (qualitativ)

Abb 5: Geladene Trennschichten zwischen Widerstand und Leiter
Diese Trennschicht vor und hinter einem Widerstand bleibt nicht neutral, wenn Elektronen durch den Widerstand getrieben werden. In der Trennschicht vor dem Widerstand (bezogen auf die Fließrichtung der Elektronen) stauen sich ein paar Elektronen, da vor ihnen ein Gebiet mit abnehmender Leitfähigkeit liegt. Diese Trennschicht wird also negativ geladen. Aus der Trennschicht hinter dem Widerstand entfernen sich ein paar Elektronen, da sich vor ihnen ein Gebiet mit gr$ouml;ßerer Leitfähigkeit befindet. In dieser Trennschicht bleiben Atomr$uuml;mpfe zur$uuml;ck, denen ein Elektron fehlt. Diese Trennschicht wird somit positiv aufgeladen.
Sowohl die unterschiedlich verteilten Ladungsträger auf den Oberflächen als auch die in den Trennschichten erzeugen abstoßende bzw. anziehende Kräfte, die die frei beweglichen Elektronen des Metalls durch den Widerstand treiben. Wird nun die Kraft an der Batterie erh$ouml;ht, so erh$ouml;ht sich der Gradient der Dichteverteilung der Oberflächenladungen, und es treten mehr unterschiedlich gepolte Ladungen vor und hinter dem Widerstand auf. Dadurch erh$ouml;ht sich die Kraft auf die beweglichen Ladungen innerhalb des Widerstandes und somit die Stromstärke, d.h. die Zahl der Ladungsträger, die pro Zeiteinheit durch einen Leiterquerschnitt fließen.
Spannung wird im deutschen Sprachraum mit U gekennzeichnet im angel-sächsischen mit V.