2.3.1. Impedance as function of induction and capacitance

A puls or a wave is transmitted on a double line, if the ratio von V/I has a specific value. This ratio is called impendence or wave resistance and is indicated as Z. It can be interpreted as some kind of resistance and is a specific property of each double line. The larger the amount of Z the more voltage is needed to transmit a pulse with a given current I.
For a dc-current we have Ohms law: R = U / I. For ac-current we have Z = U / I.
Two characteristics of a double line - the capacity and the inductance - determine the amount of the impedance Z. The meaning of these two terms and their influence on Z will be described in the next sections.

2.3.2. Capacity of a double line

As shown in chapter "2.2. Transmission processes on a double line" a voltage pulse on a double line corresponds to a certain density of additional charges at the surface of opposite line segments.

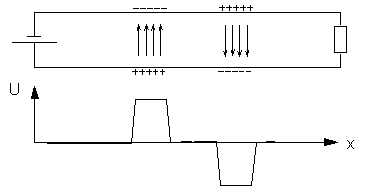
Voltage pulses and surface charges on a double line

Capacity of a line is related to the density of surface charges in relation to the applied voltage. The larger the capacity, the higher the density of surface charges for a given voltage.
There are two possibilities to change the capacity of a line and thus the density of surface charges for a given voltage. One posibility is to change the distance between the two lines, the other is to place some specific dielectric material between the two lines. Both methods have the same effect: the capacity of the line, corresponding to the density of surface charges for a given voltage, is changed.
Further explanations are found under Capacity as function of distance and Capacity and dielectric material

2.3.3. Inductance of a double line

In case of a flow of gas in a tube it seems plausible that gas with different inertial mass will need a different driving force. A gas like hydrogen with molecules, which have 8 times less mass than Oxygen molecules, will start moving much faster than oxygen gas, and can easierly be stopped.
For an electric current an inert behaviour can also be found. However, this effect is not related to the mass of the electrons. The mass is the same for all electrons - there are no "hydrogen" electrons or "oxygen" electrons - and effects due to this mass are so small that they can be neglected.
Electrons are surrounded by an electric field and are impeding each other when ever they are accelerated. The more electrons are starting to move or are changing their drift velocity and the closer they are, the more they are impeding each other. This is a fundamental electric effect, that cannot be explained with mechanical concepts. For a deeper understanding you have to refer to corresponding text books under the headline ,Electromagnetic Induction".
To follow the description below it is sufficient to know that on a double line there exists a kind of inertia for electrons. This inertia will allways show up if the drift velocity of electrons is changed or, more general, if the current is changed.
This inertial like property of a double line is called inductance and is indicated by the letter L. As with the capacity C, the inductance of a double line can be changed by either changing the distance between the conductors or by introducing specific material with magnetic properties between the conductors.
Inductance as function of distance and Inductance and magnetic material

2.3.4. Relation between Z, L and C

Qualitative description
When increasing the inductance of a double line, a given voltage V will produce a smaller current I because the impeding interaction between the electrons is increased. Therefore the ratio Z= V/I is increased. When increasing the capacitance of a double line, some additional electrons are necessary to keep up a given voltage. Therefore the current I is increased in relation to V, corresponding to a decrease of Z = V/I.

Quantitative formulation
Derived by theory and proven by experiment the relation between L, C and Z is: Z = √L/C.
If L is measured in Henry and C in Farad the unit for Z is Ohm.
For the impedance Z of a double line it is therefore of no importance if for instance the capacity is reduced by a factor of 2 or the impedance is doubled. Another example: If the capacitance and the inductance are both changed by the same factor, the impedance remains unchanged.
Both L and C depend on the distance between the two lines.So If L and C are to be changed independently of one another, this is only possible through the introduction of appropriate materials (dielectrica for the change of C, magnetic material for the change of L )

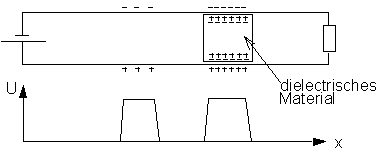
2.3.5. Double line with variable capacity

The simulations program TL offers the possibility to vary the value for C for the complete line without changing L. This is realized in an experimental setup by placing dialectric material between the lines.

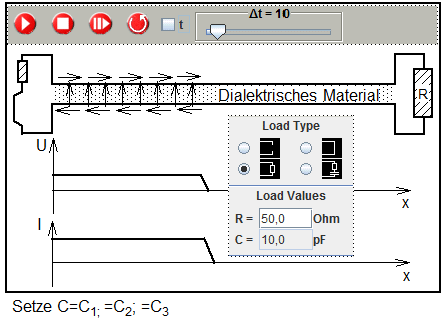
Wave front on a double line with variable capacitance
(prepared simulation: 2-3-5-line-mit-Z=40-Ohm.xml)

After starting the simulation a wave front is moving along the line where the ratio Z=V/I varies with C.
The numerical value for Z can be found by determining the resistance of the load with no reflection. The numerical value for the resistance of the load can be entered in the corresponding dialog window.

2.3.6. Double line with variable inductivity

The simulations program TL offers the possibility to vary the value for L for the complete line without changing C.
This is realized in an experimental setup by placing magnetic material between the lines.

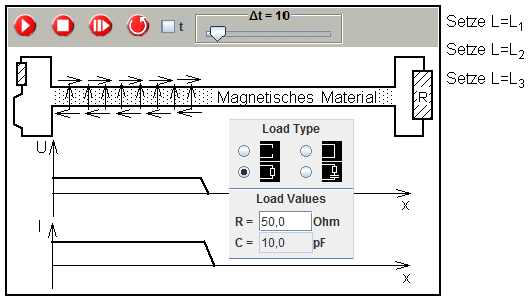
Wave front on a double line with variable inductivity
(prepared simulation: 2-3-6-line-mit-Z=90 Ohm.xml)

After starting the simulation a wave front is moving along the line where the ratio Z=V/I varies with L. The numerical value for Z can be found by determining the resistance of the load with no no reflection. The numerical value for the resistance of the load can be entered in the corresponding window.

Capacity as function of distance

When changing the distance of the conductors of a double line, the Coulomb forces between the surface charges of opposite polarity are changed. The smaller the distance, the larger the attractive forces. This implies that for a given voltage a larger density of surface charges will be established and vice versa.

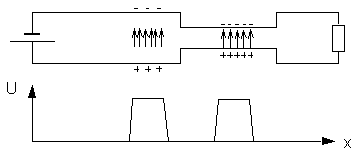
Electric double line and circuit diagram

Capacity and dielectric material

Within isolators the electrons cannot move freely but are fixed to the atoms or molecules which form the lattice of the material. Under the influence of an electric field, however, the electrons can change their position slightly in respect to the positive charges of the atoms. This slight displacement results in electric dipoles, formed by each single atom. Such a property is called dielectric.
If such a dielectric material is inserted between the conductors of a double line, this material is influenced by any existing surface charges and is reacting back on such charges.
Due to their electric field surface charges on a conductor will force the dielectric material to form atomic or molecular dipoles. These atomic dipoles will be oriented in such a way that surface charges on the conductor are faced with a layer of opposite charges formed by the dipoles within the dielectric material.

Density of surface charges with and without dielectric material between the lines