2.2.1. Reflection at an open end (R = ∞ Ω)

In analogy to the mechanical case we can expect a reflection, if a voltage/current pulse or a wave front is reaching the terminating resistor, the so-called load, at the end of a double line.
A double line with an open end corresponds to a load with R = ∞
The following figures shows such a case with a pulse just before hitting the open end and at the moment of reflection.

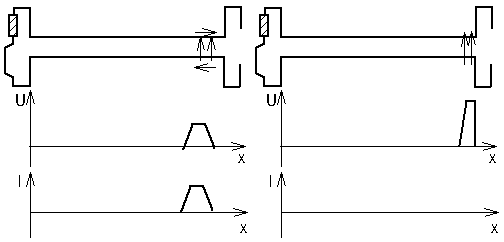
Left: A pulse moving towards the open ends of a double line (R = ∞ Ω)
Right: Moment of reflection

When arriving at the interruption the current is stopped while the height of the voltage pulse is increased and its width decreased. When the current has come to a complete stop only a zone with increased voltage on the line remains.
As shown in chapter "2.2.4. Displacement of a voltage pulse on a double line" such a pulse would split in two parts, spreading out to both sides with equal width and reduced height.
In the actual situation, however, the transmission to the right is not possible because of the infinite resistor, the open endings. Therefore the part originally send to the right will be reflected to the left. As a result we get a reflection of the original pulse with same height and width.
The simulation allows to observe this process in detail.

(vorbereitete Simulation: 2-2-1-Puls-R-infinit.xml)

2.2.2. Reflection at a short circuit as terminating resistor

If the two endings of a double line are directly connected, a so-called short-circuit is formed. R = 0 Ω.
The following figures shows such a case with a pulse just before hitting the open end and at the moment of reflection.

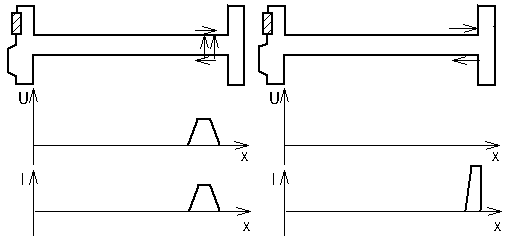
Left: A pulse moving towards the shorted ends of a double line (R=0 Ω)
Right: Moment of reflection

At the place where both lines are directly connected the surface charges on both lines of different polarity are approaching and neutralizing each other. While approaching the mutual Coulomb interaction is increasing, leading to an increased velocity of the drifting electrons.
In the middle of the reflection process no extra charges are left on the surface (V=0), however, a zone of drifting electrons exists.
This situation and the following process corresponds to the description given in chapter "2.2.5. Displacement of a zone with drifting electrons on a double line".
Such a zone will normally split into two parts and separate to both sides. At the end of a shorted double line, however, the two parts are moving back towards the source on the two separated lines.
The simulation allows to observe this process in detail.

(vorbereitete Simulation: 2-2-2-puls-R-zero.xml)

2.2.3. Terminating resistor for no reflection

In a mechanical closed system a terminating resistor with a specific value could be found which did not cause reflection for any arriving pulse or wave front. The condition was that this resistor should not change the ratio ΔP/I during the reflection process.
It can be assumed that a similar condition will hold for an electric double line, where the terminating resistor will not change the ratio V/I and will therefore not cause any reflection.
The simulation allows to observe the reflection for various values of R and to determine this so-called matched resistor value for no reflection.

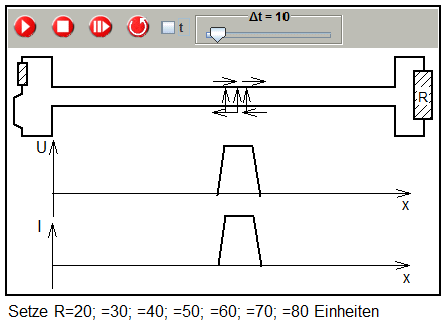
Simulation of a pulse transmission and reflection on a double line
Simulation of a pulse transmission and reflection on a double line
(vorbereitete Simulation: 2-2-3-puls-R-50Ohm.xml)

The ratio V/I, which is necessary for the transmission of a pulse or wave front is a property of the related line. It has been given the name impedance, its symbol is Z and it is measured in Ohm. (Ω).

This ratio (V/I measured in Ohm) is at the same time the condition for a current to flow through an ohmic resistor.
Based on these facts it can be assumed - and the simulation will confirm this assumption - that for a double line with impedance Z and a terminating resistor R=Z there will be no reflection. Theory and experiment confirm this supposition.
n all other cases (R>Z or R It may be a fruitful exercise to analyse the different kinds of reflections for either R >Z and R <<> Z and to explain the result in a similar way as it was done for R = 0 Ω and for R = ∞Ω

back to TL-tutorial (home page)