1.4.1. Closed Systems - Introduction

In addition to systems consisting of a single tube with a pump and some kind of absorber at both ends, closed circular systems are found either in nature or in the technical world, where some kind of pump drives a current through a feeding tube, then through some kind of resistor or energy transformer and through a return tube back to the pump.
Such closed circular systems are usually filled with some kind of liquid. The blood circulating system of mammals is a biological example, the central heating system is a technical one.
Since electrical systems are always based on a circular structure, such circular systems will be studied in detail in the following chapter. It is hoped that the treatment of the more concreat mechanical circular systems will serve as a good and helpful preparation for a study of the more abstract electrical systems, where electric charge carriers are moved around in a closed loop.

Closed system with feeding line, return line and terminating resistor
(prepared simulation 1-2-0-default.xml)

In the following a rather simple circular system - a so-called double line - is studied. It is assumed that the tubes, connecting the pump with the resistor are thin, long and straight and that the flow inside is linear without any turbulence. Only for these conditions a mathematical theory exists which allows to visualize the corresponding effects.

1.4.2. Pressure and current on a double line

In a double line a current (left figure) or a pulse (right figure) is caused to flow if a pump is continuously moving material from the returning line to the feeding line. To achieve this effect the pump must keep up a pressure difference between its two outlets. The pressure at the feeding line P₁ must be higher than the pressure P₂ at the returning line.

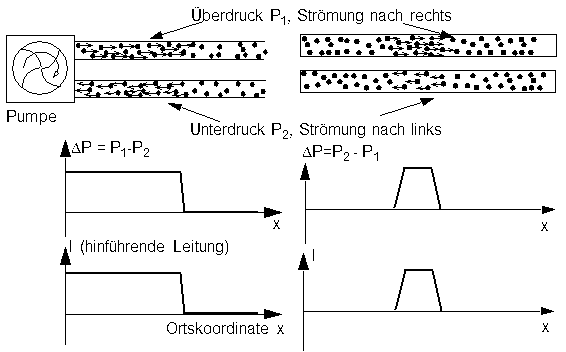
Pressure difference and current for a starting flow (left)
and a pulse(right) on a double line

In the returning line a current is produced which is directed towards the pump. In the feeding line the current is directed away from the pump. Based on symmetry arguments it can be concluded that for a given x the absolute values of current and pressure are the same on both lines.
Usually the indication of a current on a double line relates to the feeding line. The value for the returning line is equal but oriented along the opposite direction.

1.4.3. Transmission of a pulse on a double line

If the pump produced a pulse on a double line it will be transmitted to one side. This transmission process can be explained the same way as for a pulse on a single tube.
A single zone with a difference in pressure ΔP between the two line will spread out to both side.
A single zone with drifting particles (in one direction in the feeding line and in opposite direction in the returning line) will spred out to both sides.
But again the resulting pulses will cancel each other in one direction and will add up in the other direction. The final ressult is a transmission of the original pulse without change of form.

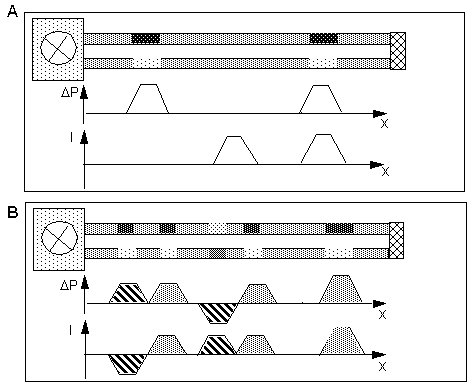
A: Starting situation: 2 separated components and a complete pulse
B: Situation after a few time steps:

The following simulation helps to study and understand this process.It is helpful to use the step button, not the run button, to activate the simulation.

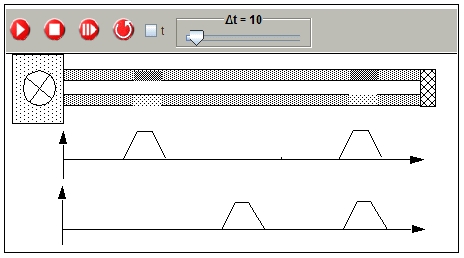
Simulation of the displacement of a pulse
and its two components at different locations
(prepared simulation 1-4-3-Puls-with-components.xml)

1.4.4. Reflection of a pulse at a terminating resistor with R =∞

The following figure shows a pulse on a double line moving towards the closed ending of the tubes.

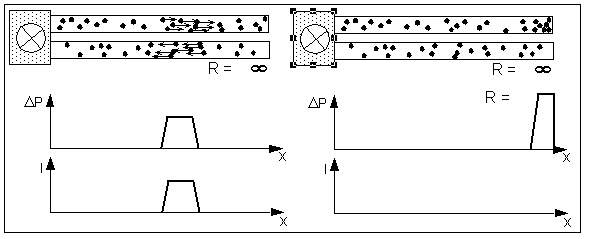
Links: Left: A pulse moving towards a closed end of a double line
Right: Moment of reflection

By the terminating end of the tube the current is stopped and a zone of inreased pressure (on the feeding line but reduced pressure on the return line) is built up in front of it.
After the current has come to a complete stop, a situation is reached which is known from chapter "1.2.5. A zone of increased pressure, changing in time". We find a single zone with increased pressure which normally should split up in two waves of half size, moving to both sides. The displacement to the right is blocked by the closed end of the pipe and therefore this part is reflected and also displaced to the left. The total result is a reflected pulse of same width and height.
The simulation shows the result of the reflection process.

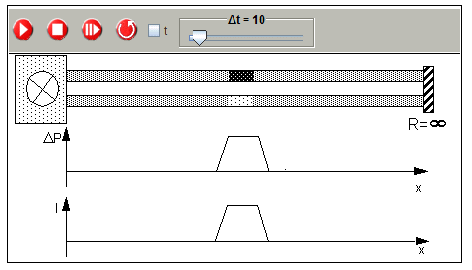
Simulation of a pulse reflection at a closed end of a double line (R = ∞
(prepared simulation 1-4-4-Puls-R-infinit.xml)

1.4.5. Reflection of a current step at a terminating resistor with R =∞

The following figure shows the front of a continuous current moving towards the closed ending of the tubes.

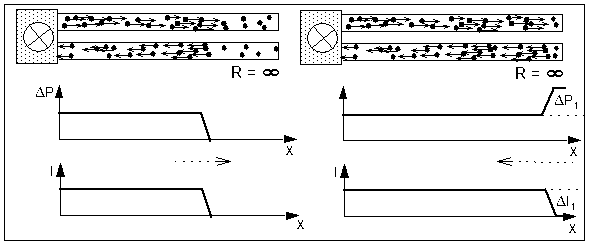
Left: The front of a current moving towards a closed end of a double line
Right: Moment of reflection

The continuous current will come to a halt in front of the resistor by producing an increased pressure. The shoulder formed by ΔP₁ and -ΔI₁ will be transmitted backward to the pump and will bring the complete current to a halt.
The simulation demonstrates this process of reflection .

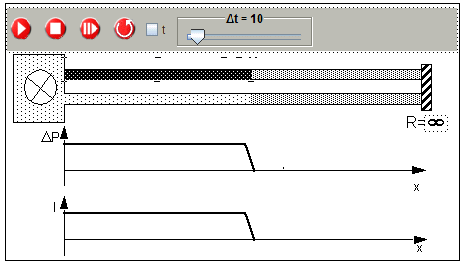
Simulation of a current moving towards the closed
Simulation of a current moving towards the closed ∞
(prepared simulation 1-4-5-current-step-R-infinit.xml)

1.4.6. Reflection of a pulse at a terminating resistor with R=0

The following figure shows a pulse on a double line moving towards the ending of the double line where the tubes are connected with practically no resistance.

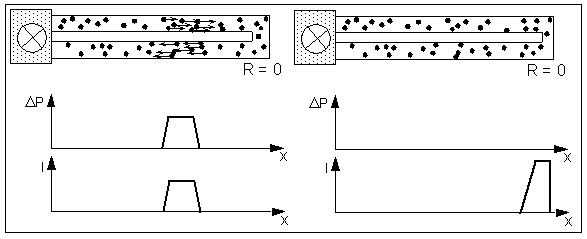
Left: A pulse moving towards the shorted ends of a double line
Right: Moment of reflection
(prepared simulation 1-4-6-Puls-R-zero.xml)

When a pulse reaches the ending of the double line with R=0, the difference in pressure will vanish during the reflection process, but the velocity of the particles will increase.
The situation in the middle of the reflection process is similare to the situation, discussed in chapter "1.2.6. A zone with drifting particles, changing in time". The current puls (without any ΔP) at the shorted endings of the double line will spread out to both sides, leading to a puls in backward direction with a change in sign of I and ΔP. .

1.4.7. Reflection of a current step at a terminating resistor with R = 0

The following figure shows the front of a continuous current moving towards the ending of a double line with R = 0.

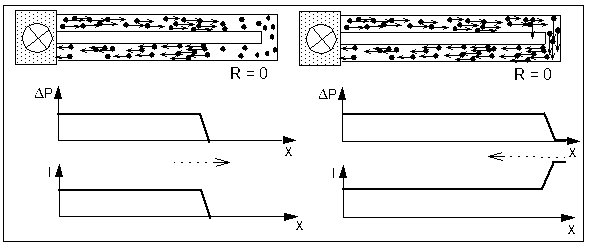
Left: The front of a current moving towards the shorted ends of a double line
Right: State of pressure and current at the moment of reflection
(prepared simulation 1-4-7-current step-R-zero.xml)

If a current step, caused by a starting pump, is reaching the shorted end of a double line, the pressure differences on both lines will be compensated. This pressure equalization is causing an acceleration of the drifting particles. It increases their drift velocity,it is changing the ratio of ΔP/I and results in a current step returning to the pump.

1.4.8. Terminating resistor with no reflection

The resistor at the ending of a double line can have the specific property that the ratio of ΔP/I of an arriving pulse or wave front does not change during the reflection process. This means that during this process the drifting velocity of the particles in the feeding and returning tube and the pressure difference between these tubes have to be reduced or equalized proportionally. As a result there will be no reflection.

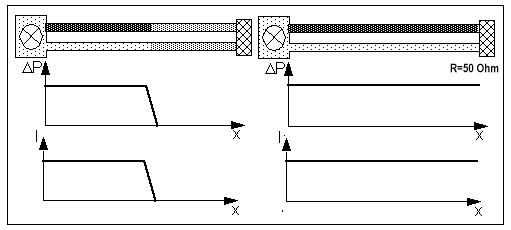
Left: Front of a current moving towards the reflection free ending of a double line
Right: State of pressure and current after "reflection"
(prepared simulation 1-4-8-current-step-R-50-Ohm.xml)

The following simulation demonstrates such a case. Sie zeigt ebenfalls den Fall einer partiellen Reflexion, sofern der Abschlußwiderstand eine Änderung des Verhältnisses von ΔP/I der eintreffenden Strömungsflanke bewirkt.

zurück zur Starseite