back to TL-tutorial (home page)
Note: All prepared simulations can be created only by mouse clicks.
To learn about the user interface of TL, see the video TL-Interface
Part 1: Transmission in mechanical systems
In analogy to an electric transmission line it is assumed that the mechanical system, which will be studied in the following, consists of a long, thin and rectilinear tube. Differences within a cross section of the tube can be neglected.
The internal gas or liquid should flow only with rather small drifting speeds so that no effect of turbulence will occur. Under such conditions the effect of transmission, superposition and reflection can be based as a first approximation on the same equations and algorithm as for the electric transmission line.
1.2.1. Representation of pressure P in abstract form
A gas under normal conditions consists of an immensely large number of molecular particles, which cannot be represented graphically. Nevertheless, it is possible to depict regions of varying pressure within a tube using abstract means instead of moving and colliding particles.
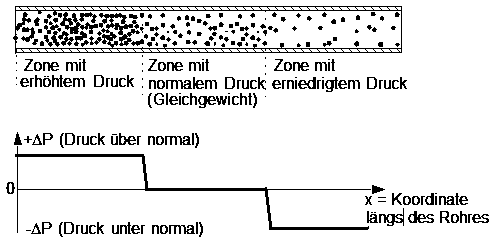
Graphical representaton of pressure along a pipe
(prepared simulation: 1-2-1-pressure-abstract)
The horizontal axis of the graph represents the position in the direction of the pipe. The vertical axis represents the pressure.
A pressure of zero units within a gas is only possible if the tube is empty or if there is no thermal velocity of the gas atoms or molecules i.e. at 0 o Kelvin. Under normal conditions a pressure always exists within a gas.
For practical reasons the pressure which exists at equilibrium is set to zero. Pressure above or below normal is then indicated as +ΔP and -ΔP respectively.

Graphical representaton of pressure along a pipe
(prepared simulation: 1-2-1-pressure-abstract)
1.2.2. Representation of current I in abstract form
If a flow of gas through a tube has to be represented, it is practically impossible to do so by showing the motion of the individual particles. The drifting velocity of the particles in the direction of the tube is - as a rule - much smaller than the thermal velocity and therefore could not be visualized. Again we shall use a more abstract form to represent a flow of gas.
This is introduced in the following diagram.
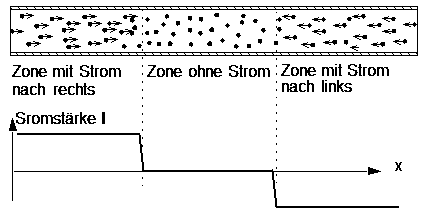
Graphical representaton of currrent
(prepared simulation 1-2-2-current-abstract.xml)
The horizontal axis of the graph represents the position along the pipe, as before. The vertical axis represents the drift velocity or current (positive for a current to the right, negative for a current to the left).

Graphical representaton of currrent
(prepared simulation 1-2-2-current-abstract.xml)
1.2.3. Positive and negative direction of transmission
Positive and negative numbers can be arranged on a straight line where the sign of the numbers indicates the direction in which the number has to be placed in respect to the zero point.
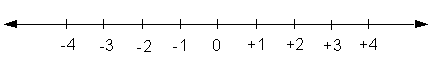
Positive and negative numbers as indication of orientaton along a given direction
In the same way the direction of a current can be determined but only if the current is flowing in parallel to a pre-defined direction. Any such direction has two opposite orientation which are usually named as positive and negative. The same holds for the orientation of a current, as long as it is flowing parallel to a given direction.
Positive and negative numbers as indication of orientaton along a given direction
1.2.4. Transmission of a pulse
A pulse inside of tube represents a zone with higher pressure (higher density of particles), where the particles within this zone have a common drift velocity in one direction.

Transition of a pulse along a tube filled with gas or liquid
It seems to be quite natural that such a pulse is transmitted along the tube with constant velocity and without changing its form. It also seems to be normal that a pulse, when hitting the end of the tube, is either reflected, or partly or completely absorbed.
The following prepared simulations demonstrate such processes as well as the superposition of two pulses.
Propagation of a pulse with complete absorption without reflection:1-2-4-puls-absorption,xml
Propagation of a pulse with full reflection and no absorption: 1-2-4-reflection.xml
Propagation of a pulse with partial reflection and partial absorption: 1-2-4-partial-absorption.xml
Überlagerung zweier Pulse: 1-2-4-superposition.xml
Im folgenden wird eine einheitliche Interpretation all dieser Vorgänge vorgestellt, die ein tieferes Verständnis solcher Vorgänge nicht nur in mechanischen, sondern später auch in elektrischen System ermöglicht.

Transition of a pulse along a tube filled with gas or liquid
1.2.5. A zone of increased pressure, changing in time
The following figure to the left shows one component of a pulse, a zone with higher pressure To the right is indicated what will happen after a few time steps after the equalization process has been started.
It is assumed that this unstable situation has been created in a rather short time. On the right is indicated what will happen a few time steps after the equalization process has been started.
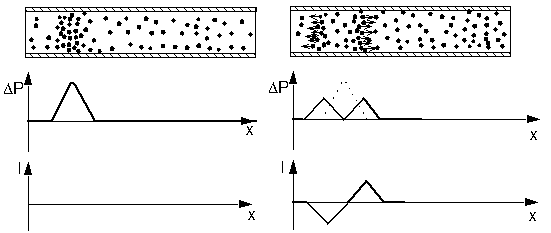
Displacement of a small zone with drifting particles
left: Starting position
right: Position after a few time steps
The particles inside of the compressed zone will exert a stronger push on their neighbours on both sides than these can push back. The zone will therefore spread out to both sides, one half starting to move to the right, the other half starting to move to the left.
The diagram indicates this drift velocity by arrows connected to the moving particles. The random velocity, which is usually much larger than the drift velocity, is not shown, although it is of vital importance for the equalization process to occur.
The simulation allows to study this process in detail, by activating the simulation with the step button  not with the run button.
not with the run button.
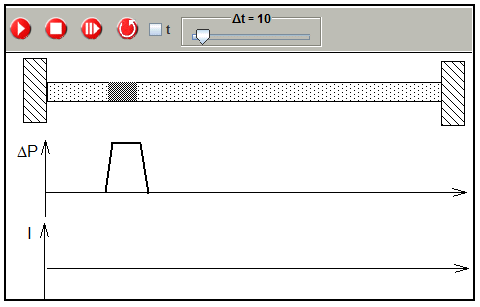
Simulation of the displacement an small pressure zone
(prepared simulation: 1-2-5-pressure.xml)
1.2.6. A zone with drifting particles, changing in time
The following figure to the left shows a second component of a pulse, a zone where the particles are drifting in one direction with no increase or decrease of pressure, while the particles outside of this zone are still at rest.
It is assumed that this unstable situation has been created in a rather short time. On the right is indicated what will happen a few time steps after the equalization process has been started.
Displacement of a small zone with drifting particles
left: Starting position
right: Position after a few time steps
In this case there is again a reaction to both sides
AOn the right side the drifting particles will cause an increased pressure zone. Because of the unavoidable collision processes they will transmit their driftvelocity to the particles in this zone.
On the left side (opposite to the drifting velocity) the drifting particles will leave a depletion zone. The particles within this zone will start drifting to the right, because they experience more collisions from their left neighbours than from the right side, where the particles are drifting away.
This process of can be studied in detail with the following simulation.
Simulation of the propagation of a zone with drifting particles
but no change in pressure
(prepared simulation: 1-2-6-drift.xml)
Again it is advised to activate the simulation by using the step button
1.2.7. Transmission of a pulse - a new interpretation
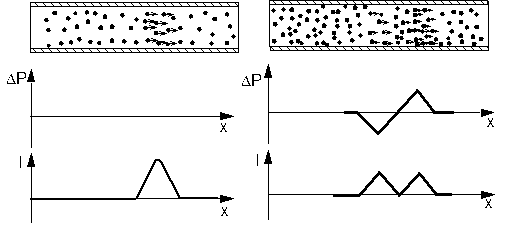
If the two components of a pulse, a zone with increased pressure and a zone with drifting particles are compared and superimposed - see next picture - it becomes obvious, while a pulse it transmitted to one side without changing its form.
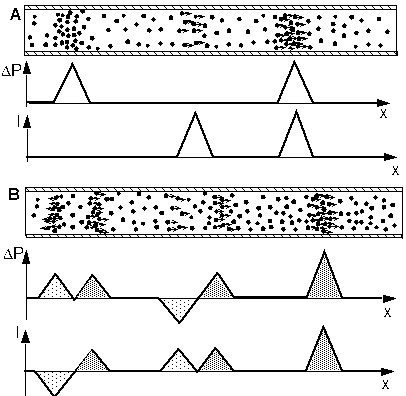
A: Starting situation: A pulse and its components at different locations
B: Situation after a few time steps:
Propagation to both sides and pulse transmission
As indicated graphically the propagation of the separated components cancel each other on the left side and add up on the right side. The result is a simple transmission of the original pulse to the right without changing its form.
The simulation allows to study this process in details.
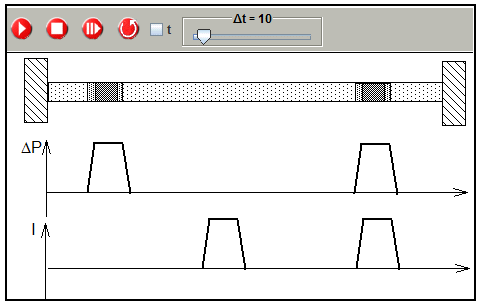
Simulation of the displacement of a pulse and its two components
(prepared simulation: 1-2-7-puls-with-components.xml)
Again it is strongly advised to activate the simulation by using the step button, not the run button.
1.2.8. Direction of transmission
The previous simulation demonstrated that the movement of a pulse can be explained as the superposition of two effects: one induced by an increased pressure zone (ΔP) and the other induced by a zone with drifting particles (I).
Until now both, ΔP and I were positive, resulting in a pulse or wave front moving in the direction of drifting particles, in our case to the right.
The simulations allows to find out what will happen if ΔP and I have negative or opposite signs.
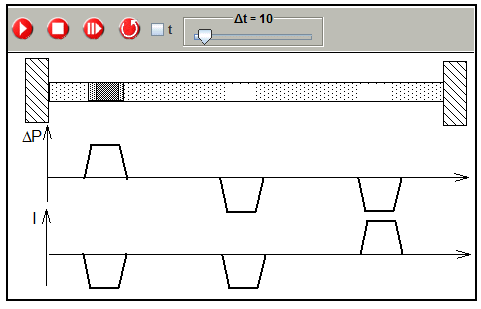
Simulation of pulse transmission in opposite directions
(prepared simulation: 1-2-8-puls-to-right.xml; 1-2-8-puls-to-left.xml)
The result showed by the simulation can be expressed in form of a simple rule:
If ΔP and I are both either positive or negative, the pulse is transmitted in the positive direction. If ΔP and I have opposite signs, the pulse is transmitted in the negative direction.
It may be an interesting activity to study the case of a pulse with -ΔP and -I in detail like in the previous chapter 1.2.7., to understand, why a pulse is transmitted in the positive direction, even so the particles are drifting in the negative direction.
In the editing mode new values for ΔP and I can be adjusted by displacing the small mouse-sensitive squares.
1.2.9. Pulse transmission for an arbitrary ratio of ΔP/I
Based on the previous chapters, two basic results can be formulated.
1. A pulse can be divided into a zone with an increased or decreased pressure (ΔP) and into a zone with drifting particles (I).
2. The transmission of a pulse is a result of the propagation of these two components in both directions.
For the cases discussed in the previous chapters the ratio of ΔP/I was chosen in such a way that the propagation of ΔP and I canceled in one direction and added up in the opposite direction to reproduce the original pulse at a dispaced position. This, however, is only possible, if the ratio of ΔP/I has a specific value.
The following figure shows a situation where the ratio ΔP/I has been arbitrarily chosen and where the two components together with the pulse are displaced at separate locations.
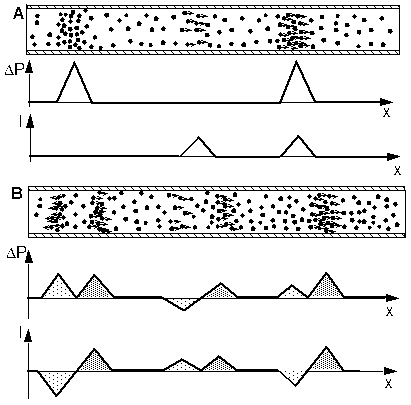
Displacement of a pulse with a changed ratio of ΔP/I
The situation after a few time steps is shown in the lower part (Fig. B). Due to the actual ratio of ΔP/I the two propagation processes to the left side do not cancel as before. The supersposition of these two propagation processes results in a division of the original pulse moving in opposite directions. .
Again, it appears that the result can be interpreted as a superposition of the dispersion process to both sides of both parts, the zone of increased pressure and the zone with drifting particles.
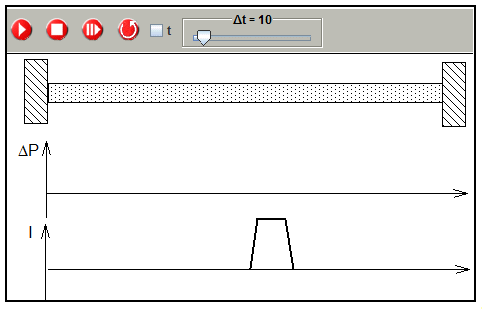
The simulation allows to study this process in detail.
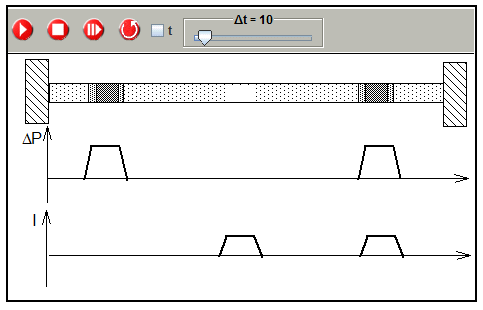
Simulation of the displacement of a pulse with a changed ratio of ΔP/I
(prepared simulation: 1-2-9-puls-with-different-components.xml)
In edit mode new values for ΔP and I can be set by moving the mouse-sensitive little squares.
By using different starting situation for ΔP and I it can be checked whether the rule, stated above, is valid in general
zurück zur Starseite

Displacement of a small zone with drifting particles
left: Starting position
right: Position after a few time steps

Simulation of the displacement an small pressure zone
(prepared simulation: 1-2-5-pressure.xml)

Displacement of a small zone with drifting particles
left: Starting position
right: Position after a few time steps
AOn the right side the drifting particles will cause an increased pressure zone. Because of the unavoidable collision processes they will transmit their driftvelocity to the particles in this zone.
On the left side (opposite to the drifting velocity) the drifting particles will leave a depletion zone. The particles within this zone will start drifting to the right, because they experience more collisions from their left neighbours than from the right side, where the particles are drifting away.
This process of can be studied in detail with the following simulation.

Simulation of the propagation of a zone with drifting particles
but no change in pressure
(prepared simulation: 1-2-6-drift.xml)

A: Starting situation: A pulse and its components at different locations
B: Situation after a few time steps:
Propagation to both sides and pulse transmission
The simulation allows to study this process in details.

Simulation of the displacement of a pulse and its two components
(prepared simulation: 1-2-7-puls-with-components.xml)
Until now both, ΔP and I were positive, resulting in a pulse or wave front moving in the direction of drifting particles, in our case to the right.
The simulations allows to find out what will happen if ΔP and I have negative or opposite signs.

Simulation of pulse transmission in opposite directions
(prepared simulation: 1-2-8-puls-to-right.xml; 1-2-8-puls-to-left.xml)
If ΔP and I are both either positive or negative, the pulse is transmitted in the positive direction. If ΔP and I have opposite signs, the pulse is transmitted in the negative direction.
It may be an interesting activity to study the case of a pulse with -ΔP and -I in detail like in the previous chapter 1.2.7., to understand, why a pulse is transmitted in the positive direction, even so the particles are drifting in the negative direction.
In the editing mode new values for ΔP and I can be adjusted by displacing the small mouse-sensitive squares.
1. A pulse can be divided into a zone with an increased or decreased pressure (ΔP) and into a zone with drifting particles (I).
2. The transmission of a pulse is a result of the propagation of these two components in both directions.
For the cases discussed in the previous chapters the ratio of ΔP/I was chosen in such a way that the propagation of ΔP and I canceled in one direction and added up in the opposite direction to reproduce the original pulse at a dispaced position. This, however, is only possible, if the ratio of ΔP/I has a specific value. The following figure shows a situation where the ratio ΔP/I has been arbitrarily chosen and where the two components together with the pulse are displaced at separate locations.

Displacement of a pulse with a changed ratio of ΔP/I
Again, it appears that the result can be interpreted as a superposition of the dispersion process to both sides of both parts, the zone of increased pressure and the zone with drifting particles.
The simulation allows to study this process in detail.

Simulation of the displacement of a pulse with a changed ratio of ΔP/I
(prepared simulation: 1-2-9-puls-with-different-components.xml)