zurück zur Startseite
Fallen und Werfen - Gravitationsgesetz
5.1. Gewicht und Gewichtslosigkeit
 Abb. 5.1.: Ist das Kind gewichtslos?
Abb. 5.1.: Ist das Kind gewichtslos?
In der Mitte des 17. Jahrhunderts formulierte Newton das universale Gravitationsgesetz, das aussagt, dass alle materiellen Körper miteinander wechselwirken in Form gegenseitiger Anziehung (siehe Abschnitt 5.2.)).
Auf Grund der Gravitationswechselwirkung mit der Masse der gesamten Erde besitzt jeder Körper hier auf der Erde ein bestimmtes Gewicht.
Wie entstehen aber Bedingungen für Gewichtslosigkeit? Hat das Kind auf dem Photo ein Gewicht oder ist es gewichtslos? Ist es nur in diesem Augenblick ohne Gewicht oder während des gesamten ,Wurfes"?
Diese Fragen und andere, die sich auf Bewegungen unter dem Einfluß der Erdanziehung beziehen, werden im folgenden behandelt.
 Abb. 5.1.: Ist das Kind gewichtslos?
Abb. 5.1.: Ist das Kind gewichtslos?
5.2. Gravitationsgesetz
Qualitative Beschreibung
Das Phänomen der Massenanziehung, auch Gravitation genannt, besagt, dass alle materiellen Körper sich gegenseitig anziehen. Aufgrund dieser Tatsache werden alle Körper von der Erde angezogen und haben somit ein Gewicht. Dieses zwar sehr alltägliche Phänomen ist im Grunde sehr erstaunlich und bis heute haben die Physiker dafür keine Erklärung gefunden. Es muß als ein nicht erklärbares Grundphänomen hingenommen werden.
Die anziehende Kraft zwischen zwei Körpern 1 und 2 ist proportional zu einer bestimmten Eigenschaft dieser Körper, die man versuchsweise zunächst als "Gravitations-Eigenschaft" bezeichnen kann
Es hat sich experimentell gezeigt, dass diese Eigenschaft unter allen Umständen proportional ist zu der schon weiter oben eingeführten Größe "Masse". Diese Tatsache ist zunächst sehr erstaunlich, denn es gibt keinen erkennbaren Zusammenhang zwischen der Eigenschaft eines Objekts, einer Beschleunigung einen Widerstand entgegenzusetzen, seiner Trägheit, und der Eigenschaft, andere materielle Körper anzuziehen.
Einstein hat in seiner Theorie der Allgemeinen Relativität einen Zusammenhang zwischen diesen beiden Eigenschaften materieller Körper hergestellt. Diese Ableitung ist jedoch nur für Fachleute nachvollziehbar.
Es gibt andere mehr spekulative Erklärungen, welche die Trägheit auf eine Gravitationswechselwirkung mit den Sternen im gesamte Kosmos reduzieren.
Es wird jedoch generell akzeptiert, dass aus der allgemein gültige Proportionalität zwischen der Trägheit und der oben versuchsweise so bezeichneten Gravitations-Eigenschaft folgt, dass beide Größen einen gemeinsamen Ursprung haben. Aus diesem Grund werden beide Größen mit dem gleichen Namen "Masse" gekennzeichnet und in den gleichen Einheiten gemessen. Um zwischen diesen beiden Größen unterscheiden zu können, spricht man auch von "träger Masse" mt und "schwerer Masse" ms.
Quantitative Beschreibung
Als ein universelles Gesetz gilt: Alle materiellen Körper ziehen sich gegenseitig an.
Die anziehende Kraft F zwischen zwei materiellen Körpern 1 und 2 ist zunächst abhängig von der schweren Masse der sich anziehenden Körper m(s)1
und m(s)2. Die Kraft hängt außerdem vom Abstand der beteiligten Körper ab, und zwar ist die Größe der Anziehungskraft umgekehrt proportional zum Quadrat des Abstandes der Mittelpunkte beider Körper.
In quantitativer Form lautet das Gravitationsgesetz:

Die Konstante γ ist eine universelle Naturkonstante.
5.3. Körper im freien Fall
Sieht man von der Luftreibung ab, so erfahren alle Körper beim Fallen unabhängig von ihrem Gewicht die gleiche Beschleunigung.
Das unter Fall-Experiment von 3 Körpern mit unterschiedlicher Masse herunterzuladende Video zeigt ein Experiment, in dem drei sehr unterschiedliche Bälle aus einer Höhe von ungefähr 4m fallen gelassen werden.
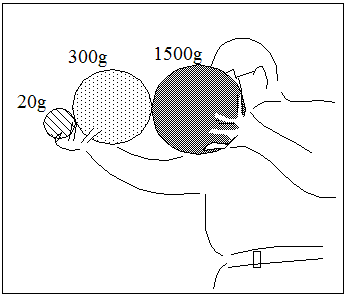



Abb. 5.2.: Video von einem Fall-Experiment von 3 Körpern mit unterschiedlicher Masse.
Für viele Menschen ist das Ergebnis eher selbstverständlich. Sie halten die Tatsache, dass alle Körper gleich schnell zu Boden fallen, für ein Naturgesetz. Es gibt aber auch viele Menschen, die davon überzeugt sind, dass leichte Körper langsamer fallen als schwerere.
Jedoch gibt es dort ein merkwürdiges Problem. Ein leichterer Körper wird mit einer viel kleineren Kraft von der Erde angezogen als ein schwererer. Warum legen beide Körper dennoch in der gleichen Zeitdauer die gleiche Fallstrecke zurück, erfahren also die gleiche Beschleunigung?

Abb. 5.3.: Simulation "freier_Fall"
Um eine befriedigende Antwort auf die obige Frage zu finden, muß man beachten, dass bei einer Fallbeschleunigung nicht nur das Gewicht und damit die schwere Masse von Bedeutung ist, sondern auch die träge Masse.
In jedem Fall gilt: Je schwerer ein Körper ist, desto größer ist seine träge Masse und umgekehrt.
Da diese beiden Größen streng zueinander proportional sind, heben sie sich in ihrer Wirkung auf die Fallbeschleunigung gegenseitig auf. Somit erfahren alle materiellen Körper die gleiche Fallbeschleunigung.
5.4. Fallstrecke und Falldauer
Alle Körper erfahren unabhängig von ihrer Masse die gleiche Fallbeschleunigung. Dies hat zur Folge, dass der Zusammenhang zwischen Fallstrecke und Fallzeit für alle Körper unabhängig von ihrer Masse gültig ist.
Für den einfachen Fall, dass ein Körper ohne Anfangsgeschwindigkeit fallen gelassen wird, lautet diese Beziehung:
s = 1/2 g t2
s = Fallstrecke; g = Fallbeschleunigung; t = Fallzeit
Die Fallstrecke wächst quadratisch mit der Fallzeit an.
Die Simulation ""5-Fallweg_Fallzeit"" veranschaulicht, wie diese Formel abgeleitet werden kann.

Abb. 5.4.: Simulation "5-Fallweg_Fallzeit"
Vergleich der Bewegung 2er Teilchen mit konstantem v und konstantem a
In dieser Simulation wird ein elektrisches Feld in -z-Richtung (nach unten) simuliert, aber kein Gravitationsfeld. Da das rechte Teilchen eine Ladung trägt, bewegt es sich unter der Wirkung einer konstanten elektrischen Kraft mit konstanter Beschleunigung. Das linke neutrale Teilchen bewegt sich wegen seiner Startgeschwindigkeit
v0 geradlinig gleichförmig.
Die Geschwindigkeit des beschleunigten Körpers wächst von Null linear an bis zu einem maximal Wert vmax im Augenblick des Auftreffens auf den Boden.
Frage: Wie groß muß v0 gewählt werden, damit beide Teilchen im gleichen Augenblick den Boden erreichen?
Die Geschwindigkeit des linken Teilchens kann im "Teilchen Inspektor"-Fenster geändert werden (Abb. 3.1)
Antwort:
Um in der gleichen Zeitdauer die gesamte Fallstrecke smax zurückzulegen, muß sich der linke Körper mit der konstanten Geschwindigkeit v = vmax/2 bewegen. Dann ist er auf der ersten Wegstrecke zunächst zu schnell, aber danach auf der zweiten Wegstrecke zu langsam. Dies gleicht sich nach der Zeitdauer t
max aus, da die Geschwindigkeit des rechten Körpers von v = 0 linear bis v = vmax ansteigt.
Die vom linken Körper mit der konstanten Geschwindigkeit v = vmax/2 in der Zeitdauer tmax zurückgelegte Wegstrecke beträgt

Wegen der konstanten Beschleunigung g gilt für die Geschwindigkeit des rechten Körpers:vmax = g tmax.
Durch Einsetzen erhält man:

Solange der Körper aus der Ruhe startet gilt diese Überlegung für jede beliebige Fallstrekke und Falldauer. Deshalb kann der Index weggelassen werden und man erhält, wie oben angegeben, als Beziehung zwischen Fallstrecke und Falldauer:
s = 1/2 g t2
Die Simulation "5-Fallweg_Fallzeit" mit den Parametern smax = 2000 Einheiten;
g = 10 Einheiten zeigt eine Übereinstimmung mit der obigen Ableitung (mit v = vmax/2).

Abb. 5.4.: Simulation "5-Fallweg_Fallzeit"
Vergleich der Bewegung 2er Teilchen mit konstantem v und konstantem a


5.5. Schwerelosigkeit und Kräftefreiheit - Ein wichtiger Unterschied
Wenn man im Fernsehen sieht, wie Astronauten durch ihr Raumschiff schweben während sie um die Erde kreisen, dann ist es offensichtlich, dass sie schwerelos sind. Aber sind sie auch kräftefrei?
Sicherlich nicht, denn diese Raumschiffe bewegen sich im Gravitationsfeld der Erde. Für normale Umlaufbahnen ist dieses Feld nahezu gleich stark wie hier auf der Erde.
Das gleiche gilt für einen Körper im freien Fall. Dieser ist ebenfalls nicht kräftefrei aber er ist schwerelos. Sonst würden Wissenschaftler nicht einen so genannten Fallturm betreiben wie an der Universität Bremen, in dem Versuche unter der Bedingung der Schwerelosigkeit durchgeführt werden.
Das unter Fallturm in Bremen "herunterzuladende Video zeigt diesen Fallturm und stellt eine interessante Frage hinsichtlich der Schwerelosigkeit beim senkrechten Wurf aufwärts.


Abb. 5.5.: Video über den Fallturm in Bremen
Unterschied zwischen Schwerelosigkeit und Kräftefreiheit
Antwort:
Ein Körper hat ein Gewicht, wenn er sich im Gleichgewicht zwischen zwei Kräften befindet, der Erdanziehungskraft, die nach unten zieht und einer aufwärts gerichteten Gegenkraft, die vom Boden oder der Unterlage aufgebracht wird.
Auf Grund dieser beiden entgegengesetzt orientierten Kräfte wird ein Körper je nach seiner Elastizität mehr oder weniger deformiert. Diese elastische Verformung verschwindet, wenn keine Gegenkraft durch den Boden einwirken kann, sondern wenn nur die Gravitationskraft vorhanden ist, wie z.B. bei einer Fallbewegung nach unten oder einem Wurf nach oben.
Die Gravitationskraft wirkt auf jedes einzelne Atom oder Molekül eines materiellen Körpers in gleicher Weise und erzeugt deshalb keinerlei innere Spannungen oder Verformungen. Es ist dieser spannungs- und verformungslose Zustand, der für Wissenschaftler und Techniker interessant ist und deshalb werden Experimente unter Bedingungen der Schwerelosigkeit ausgeführt, sei es in einem Fallturm oder der internationalen Raumstation.
Eine nähere Erklärung, warum Astronauten in ihren Raumstationen schwerelos sind, findet sich in einem späteren Kapitel.


Abb. 5.5.: Video über den Fallturm in Bremen
Unterschied zwischen Schwerelosigkeit und Kräftefreiheit
5.6. Senkrechter Wurf
Startgeschwindigkeit und Steigzeit
Die vorbereitete Simulation "5-senkrechter_Wurf" bietet die Möglichkeit, durch Versuch und Irrtum herauszufinden, welche Startgeschwindigkeit erforderlich ist, damit der Körper entgegen der aktivierten Schwerkraft bis zur ,Decke" hochsteigt, ohne gegen sie anzustoßen. Eingestellt ist per Simulation ein konstantes senkrecht nach unten gerichtetes Gravitationsfeld.
Ein solches Gravitationsfeld kann in dem "Globale Parametereinstellungen"-Fenster aktiviert werden.


Abb. 5.6.: Simulation "5-senkrechter_Wurf";
Setzen eines externen Gravitationsfeldes in -z-Richtung
Rechnung:
Senkrechte Wurfbewegungen entweder aufwärts und abwärts sind symmetrische Bewegungen, die der gleichen konstanten Beschleunigung unterliegen.
>Deshalb gelten für beide Bewegungen die selben Gleichungen:
s = 1/2 g t2; v = g t + v0
In der obigen Simulation gilt für die Beschleunigung der Wert g = -10 Einheiten.
Stimmen Simulation und Rechnung überein?


Abb. 5.6.: Simulation "5-senkrechter_Wurf";
Setzen eines externen Gravitationsfeldes in -z-Richtung
5.7. Horizontaler Wurf
Das Experiment und eine Frage
Das Video, herunterzuladen unter Horizontaler Wurf , zeigt ein Experiment, bei dem ein Ball aus einer Höhe von etwa 4m horizontal weggestoßen wird und in einer Entfernung von etwa 6m in einen mit Wasser gefüllten Eimer trifft.


Abb. 5.7.:Video von einem horizontalen Wurf
Frage:
Angenommen ein zweiter Ball wird im gleichen Augenblick fallen gelassen, in dem der andere Ball horizontal weggestoßen wird.
Wird dieser zweite Ball den Boden vorher, zur gleichen Zeit oder später erreichen?
Mit Hilfe der Simulation "5-horizontaler_Wurf" kann eine Antwort gefunden werden.
Superpositionsprinzip
Es wäre nicht ganz so einfach, eine experimentelle Anordnung zu entwickeln, bei der zwei Bälle exakt im gleichen Augenblick fallengelassen werden, wobei der eine Ball eine variable und genau horizontale Geschwindigkeit erhält.
In einer Simulation ist diese Aufgabe dagegen sehr einfach zu erledigen. Dabei hilft das so genante Superpositionsprinzip, das besagt, dass die horizontale und die vertikale Bewegung sich nicht gegenseitig beeinflussen und daher einfach überlagert werden dürfen.
Das Superpositionsprinzip basiert auf der Tatsache, dass eine Kraft, die stets eine bestimmte Richtung aufweist, senkrecht zu dieser eigenen Richtung keinerlei Auswirkung hat.
Im vorliegenden Fall bedeutet dies, dass die Gravitationskraft die horizontale Bewegung in keiner Weise beeinflussen kann.
Diese horizontale Geschwindigkeitskomponente bleibt konstant - sie wird zumindest nicht durch die Gravitation beeinflußt, während die beschleunigte Bewegung genau so verläuft wie bei einem frei fallenden Körper ohne horizontale Geschwindigkeitskomponente.
Simulation
Wie es die Simulation "5-Horizontaler_Wurf" zeigt, erreichen die beiden Bälle gleichzeitig den Boden.
Durch Versuch und Irrtum kann man herausfinden, welche Geschwindigkeit v0
erforderlich ist, um die Kugel unten links zu treffen.
In Übereinstimmung mit dem Experiment zeigt die Simulation, dass sich die Bewegung eines horizontalen Wurfs als unabhängige Überlagerung zweier Bewegungen ergibt, nämlich einer horizontalen Bewegung mit konstanter Geschwindigkeit und einer vertikalen Bewegung mit konstanter Beschleunigung.
Rechnung
Um die vorliegende Aufgabe zu lösen, müssen die folgenden Beziehungen bekannt und verstanden worden sein:
Für eine Bewegung mit konstanter Beschleunigung gilt:
s = 1/2 g t2; v = a t; (Start aus der Ruhe)
(s = zurückgelegte Wegstrecke; v = Geschwindigkeit;g = Beschleunigung;t = Zeitdauer)
Für eine Bewegung mit konstanter Geschwindigkeit gilt:
s = v t.
Aus dem Superpositionsprinzip folgt, dass die in dem Video gezeigte Bewegung in zwei unabhängige Bewegungen aufgeteilt werden kann, und zwar in einen freien Fall mit konstanter Beschleunigung a = g und in eine horizontale Bewegung mit konstanter Geschwindigkeit.

Für den freien Fall gilt:

Für die horizontale Bewegung gilt:

Die in der Simulation eingestellten Werte sind:
s1 = 1800 Einheiten; s2 = 1800 Einheiten;g = -100 Einheiten.
Stimmen Theorie und Simulation überein?


Abb. 5.7.:Video von einem horizontalen Wurf
5.8. Schiefer Wurf
Das Experiment
Die in dem folgenden Video zu sehende, schräg gestellte Stange wird von zwei gespannten Federn gegen eine Halterung gepreßt. Wird diese Halterung gelöst, so stößt die Stange mit ihrer Spitze gegen den Ball. Nach mehreren vergeblichen Versuchen gelingt es, den Ball im Korb unterzubringen.
Die folgende Simulation gibt diesen Versuch wieder. Im Anschluß daran wird eine numerische Lösung vorgestellt.
Die Simulation

Abb. 5.10.: Simulation "5-schiefer_Wurf
Durch Variation der horizontalen und vertikalen Komponente der Startgeschwindigkeit des Balles kann man erreichen, dass der Ball im ,Korb" landet, ohne die ,Decke" zu berühren.
Eine effektivere Alternative zu Versuch und Irrtum ist der Rückgriff auf die Theorie.
Berechnung
- Für eine Bewegung mit konstanter Beschleunigung (ohne Anfangsgeschwindigkeit) gilt: s = 1/2 g t2; v = g t;
(s = zurückgelegte Strecke; v = Geschwindigkeit;g = Beschleunigung; t = Zeitdauer)
- Für eine Bewegung mit konstanter Geschwindigkeit gilt: s = v t.
Auf Grund des Superpositionsprinzips kann die in dem Video und in der Simulation gezeigte Bewegung als unabhängige Überlagerung zweier Teilbewegungen aufgefaßt werden und zwar einem senkrechten Wurf mit konstanter Beschleunigung und einer horizontalen Bewegung mit konstanter Geschwindigkeit.

Für die Aufwärts- und Abwärtsbewegung des senkrechten Wurfes gilt:

Für die horizontale Bewegung gilt:

Die in der Simulation eingestellten Werte sind (in den entsprechenden Einheiten):
s1 = 1250; s2 = 450; s3 = 1600; g = -100.
Stimmen Simulation und Theorie überein?
5.9. Eine lange, fallende Latte und ein fallender Ball im Vergleich
Experiment
In den vorangegangenen Kapiteln wurde dargelegt, dass alle Körper im freien Fall unabhängig von ihrer Masse die gleiche Beschleunigung erfahren.
Konfrontiert mit der in dem folgenden Video dargestellten experimentellen Situation könnte man daher zunächst vermuten, dass beide Körper im gleichen Augenblick auf dem Boden aufschlagen.

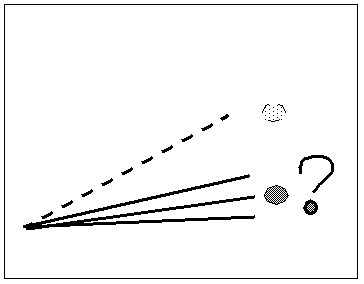
Video von einer fallende Latte und einem frei fallenden Ball
(Fallende Latte und frei fallender Ball eine Frage)
Wie das Video, herunterzuladen unter Fallende Latte und frei fallender Ball - Experiment, zeigt, wird diese Vermutung durch das Experiment widerlegt.
Das fallende Ende der Latte wird stärker beschleunigt als der frei fallende Ball. Hier muß also eine Kraft einwirken, die größer ist als die Erdanziehung.
Wie entsteht diese Kraft?
Erklärung zum Vergleich von Latte und Ball
Eine erste Antwort auf diese Frage ist recht einfach. In dem Experiment werden zwei unterschiedliche Fälle verglichen. Der Ball befindet sich ausschließlich unter dem Einfluß der Erdanziehung. Auf die schräg gestellte Latte dagegen wirkt zusätzlich zur Erdanziehung noch die Gegenkraft durch den Boden ein. Die Latte befindet sich somit nicht in einem freien Fall und somit verbietet sich ein direkter Vergleich.
>An Hand der folgenden Simulation wird die Auswirkung dieser Gegenkraft und damit der Unterschied zu einem freien Fall näher erklärt.
Simulation zum Vergleich von Latte und Ball
Die Simulation "5-fallende Latte" gibt die in dem Video dargestellte Situation wieder und erlaubt den Vergleich der Fallbewegung von Ball und schräg gestellter Latte.
In der Simulation besteht die Latte aus einzelnen Massepunkten, die mit masselosen Federn untereinander verbunden sind. Der untere linke Massepunkt ist fixiert, während die anderen Massepunkte während der Fallbewegung nicht senkrecht fallen können, sondern auf mehr oder weniger kreisförmige Bahnen um diesen Fixpunkt herum gezwungen werden.

Abb. 5.11.: Simulation "5-fallende Latte_fallender_Ball"
Auf Grund der beiden Kräfte, der Gravitationskraft und der Gegenkraft durch den Boden, wird die Latte durchgebogen. Dadurch entstehen während des Fallvorgangs anwachsende elastische Biegekräfte, die eine zusätzliche Beschleunigung bewirken.
Wird die Anzahl der Federn vergrößert und damit die Latte steifer gemacht, (Simulation "5- steife_Latte_Ball" so ist die Durchbiegung kaum noch sichtbar.
Je steifer die Latte, desto größer ist die Übereinstimmung zwischen der Simulation und dem im Video gezeigten Experiment.
5.10. Fall einer elastischen Feder?
Angenommen ein Nachbar im 1. Stock hält eine lange, weiche Feder (genannt Slinky) aus dem Fenster, so dass sich das untere Ende der Feder vor einem Fenster im Erdgeschoß befindet.
Die Frage ist: Wie wird sich das untere Ende der Feder verhalten, das man vom Erdgeschoß aus betrachten kann, und zwar in dem Augenblick in dem der Nachbar die Feder losläßt?
Wird es sich zunächst etwas nach oben bewegen, wird es für eine kurze Weile an der gleichen Stelle verharren bevor es fällt oder wird es sofort anfangen zu fallen. Diese Frage wird gestellt in dem unter Fallende elastische Feder - eine Frage herunterzuladendem Video.?


Abb. 5.12.: Video von einer fallenden elastischen Feder
Wenn man das unter Fallende elastische Feder - Experiment zu findende Video genau betrachtet, in dem das Experiment dargestellt wird, kann man erkennen, dass das untere Ende der Feder nicht sofort zu fallen beginnt, sondern erst dann, wenn sich die Feder weitgehend zusammengezogen hat.
Diesen Vorgang kann man mit Hilfe der folgenden Simulation genauer untersuchen.
Simulation

Abb. 5.13.:Simulation einer fallenden elastischen Feder
Die elastische Feder in der Simulation "5-fallende Feder" wird durch eine Reihe von Teilchen gleicher Masse dargestellt, die durch elastische Federn gleicher Federkonstante miteinander verbunden sind.
Das obere Teilchen ist fixiert.
Da eine Gravitationskraft simuliert wird, dehnt sich die Feder unter ihrem eigenen Gewicht aus.
Das einzelne Teilchen neben dem unteren Ende der Feder ist ebenfalls fixiert und kann deshalb nicht fallen.
Werden die fixierten Teilchen gelöst bevor die Simulation gestartet wird, so kann man das Verhalten des unteren Teilchens der Feder beobachten.
Soll ein Teilchen fixiert oder die Fixierung aufgehoben werden, so kann dies in dem "Teilchen Inspektor"-Fenster eingestellt werden.

Abb. 5.14.: Fixieren oder Freisetzen eines Teilchens im "Teilchen Inspektor" Fenster
Ergebnis:
Das untere Ende der Feder kann erst fallen, wenn die Feder sich fast vollständig zusammengezogen hat. Vorher ist das untere Ende nicht frei, das heißt, dass neben der Gravitationskraft noch weitere Kräfte einwirken.
5.11. Konzept des Massenmittelpunkts
Mit Hilfe der Simulation "5-Massenmittelpunkt" wird das Konzept des Massenmittelpunkts eingeführt. Dieses Konzept wird hier nicht aus grundlegenden Prinzipien abgeleitet sondern nur vorgestellt, um seine besondere Eigenschaften aufzuzeigen und um damit zu weiteren Studien anzuregen.

Abb. 5.15.: Simulation einer fallenden Feder
mit Massenmittelpunkt
Wie zuvor wird die Feder wiedergegeben als Reihe von Teilchen gleicher Masse, die mit masselosen Federn gleicher Federkonstante verbunden sind.
Das obere Teilchen ist fixiert. Da eine Gravitationskraft simuliert wird, ist die Feder auf Grund des eigenen Gewichts entsprechend ausgedehnt.
Das weiße Kreuz kennzeichnet den so genannten Massenmittelpunkt der Feder, der nach einem bestimmten Verfahren von dem Programm berechnet wird.
Das isolierte Teilchen neben dem Massenmittelpunkt kann nicht fallen, da es ebenfalls fixiert ist.
Wird die Simulation gestartet und werden die Teilchen vorher gelöst, so kann man beobachten, dass der Massenmittelpunkt genau so fällt wie das frei fallenden isolierte Teilchen.>Die allgemein gültige Regel lautet:
Der Massenmittelpunkt eines materiellen Körpers bewegt sich unter dem Einfluß einer äußeren Kraft so, als ob die Masse des ausgedehnten Körpers in ihm vereinigt wäre. Innere Kräfte spielen für die Bewegung des Massenmittelpunktes keine Rolle.
Zur Benutzerschnittstelle:
Der Massenmittelpunkt aller im Kubus gesetzten Teilchen kann im Fenster "Teilchen setzen und verwalten" aktiviert werden.

Abb. 5.16.: Aktivieren der Visualisierung
des Massenmittelpunktes
zurück zur Startseite

Abb. 5.10.: Simulation "5-schiefer_Wurf
(s = zurückgelegte Strecke; v = Geschwindigkeit;g = Beschleunigung; t = Zeitdauer)
Experiment
In den vorangegangenen Kapiteln wurde dargelegt, dass alle Körper im freien Fall unabhängig von ihrer Masse die gleiche Beschleunigung erfahren.
Konfrontiert mit der in dem folgenden Video dargestellten experimentellen Situation könnte man daher zunächst vermuten, dass beide Körper im gleichen Augenblick auf dem Boden aufschlagen.


Video von einer fallende Latte und einem frei fallenden Ball
(Fallende Latte und frei fallender Ball eine Frage)
Wie das Video, herunterzuladen unter Fallende Latte und frei fallender Ball - Experiment, zeigt, wird diese Vermutung durch das Experiment widerlegt.
Das fallende Ende der Latte wird stärker beschleunigt als der frei fallende Ball. Hier muß also eine Kraft einwirken, die größer ist als die Erdanziehung.
Wie entsteht diese Kraft?
Erklärung zum Vergleich von Latte und Ball
Eine erste Antwort auf diese Frage ist recht einfach. In dem Experiment werden zwei unterschiedliche Fälle verglichen. Der Ball befindet sich ausschließlich unter dem Einfluß der Erdanziehung. Auf die schräg gestellte Latte dagegen wirkt zusätzlich zur Erdanziehung noch die Gegenkraft durch den Boden ein. Die Latte befindet sich somit nicht in einem freien Fall und somit verbietet sich ein direkter Vergleich.
>An Hand der folgenden Simulation wird die Auswirkung dieser Gegenkraft und damit der Unterschied zu einem freien Fall näher erklärt.
Simulation zum Vergleich von Latte und Ball
Die Simulation "5-fallende Latte" gibt die in dem Video dargestellte Situation wieder und erlaubt den Vergleich der Fallbewegung von Ball und schräg gestellter Latte.
In der Simulation besteht die Latte aus einzelnen Massepunkten, die mit masselosen Federn untereinander verbunden sind. Der untere linke Massepunkt ist fixiert, während die anderen Massepunkte während der Fallbewegung nicht senkrecht fallen können, sondern auf mehr oder weniger kreisförmige Bahnen um diesen Fixpunkt herum gezwungen werden.

Abb. 5.11.: Simulation "5-fallende Latte_fallender_Ball"
Auf Grund der beiden Kräfte, der Gravitationskraft und der Gegenkraft durch den Boden, wird die Latte durchgebogen. Dadurch entstehen während des Fallvorgangs anwachsende elastische Biegekräfte, die eine zusätzliche Beschleunigung bewirken.
Wird die Anzahl der Federn vergrößert und damit die Latte steifer gemacht, (Simulation "5- steife_Latte_Ball" so ist die Durchbiegung kaum noch sichtbar.
Je steifer die Latte, desto größer ist die Übereinstimmung zwischen der Simulation und dem im Video gezeigten Experiment.


Video von einer fallende Latte und einem frei fallenden Ball
(Fallende Latte und frei fallender Ball eine Frage)

Abb. 5.11.: Simulation "5-fallende Latte_fallender_Ball"
5.10. Fall einer elastischen Feder?
Angenommen ein Nachbar im 1. Stock hält eine lange, weiche Feder (genannt Slinky) aus dem Fenster, so dass sich das untere Ende der Feder vor einem Fenster im Erdgeschoß befindet.
Die Frage ist: Wie wird sich das untere Ende der Feder verhalten, das man vom Erdgeschoß aus betrachten kann, und zwar in dem Augenblick in dem der Nachbar die Feder losläßt?
Wird es sich zunächst etwas nach oben bewegen, wird es für eine kurze Weile an der gleichen Stelle verharren bevor es fällt oder wird es sofort anfangen zu fallen. Diese Frage wird gestellt in dem unter Fallende elastische Feder - eine Frage herunterzuladendem Video.?


Abb. 5.12.: Video von einer fallenden elastischen Feder
Wenn man das unter Fallende elastische Feder - Experiment zu findende Video genau betrachtet, in dem das Experiment dargestellt wird, kann man erkennen, dass das untere Ende der Feder nicht sofort zu fallen beginnt, sondern erst dann, wenn sich die Feder weitgehend zusammengezogen hat.
Diesen Vorgang kann man mit Hilfe der folgenden Simulation genauer untersuchen.
Simulation

Abb. 5.13.:Simulation einer fallenden elastischen Feder
Die elastische Feder in der Simulation "5-fallende Feder" wird durch eine Reihe von Teilchen gleicher Masse dargestellt, die durch elastische Federn gleicher Federkonstante miteinander verbunden sind.
Das obere Teilchen ist fixiert.
Da eine Gravitationskraft simuliert wird, dehnt sich die Feder unter ihrem eigenen Gewicht aus.
Das einzelne Teilchen neben dem unteren Ende der Feder ist ebenfalls fixiert und kann deshalb nicht fallen.
Werden die fixierten Teilchen gelöst bevor die Simulation gestartet wird, so kann man das Verhalten des unteren Teilchens der Feder beobachten.
Soll ein Teilchen fixiert oder die Fixierung aufgehoben werden, so kann dies in dem "Teilchen Inspektor"-Fenster eingestellt werden.

Abb. 5.14.: Fixieren oder Freisetzen eines Teilchens im "Teilchen Inspektor" Fenster
Ergebnis:
Das untere Ende der Feder kann erst fallen, wenn die Feder sich fast vollständig zusammengezogen hat. Vorher ist das untere Ende nicht frei, das heißt, dass neben der Gravitationskraft noch weitere Kräfte einwirken.


Abb. 5.12.: Video von einer fallenden elastischen Feder

Abb. 5.13.:Simulation einer fallenden elastischen Feder

Abb. 5.14.: Fixieren oder Freisetzen eines Teilchens im "Teilchen Inspektor" Fenster
5.11. Konzept des Massenmittelpunkts
Mit Hilfe der Simulation "5-Massenmittelpunkt" wird das Konzept des Massenmittelpunkts eingeführt. Dieses Konzept wird hier nicht aus grundlegenden Prinzipien abgeleitet sondern nur vorgestellt, um seine besondere Eigenschaften aufzuzeigen und um damit zu weiteren Studien anzuregen.

Abb. 5.15.: Simulation einer fallenden Feder
mit Massenmittelpunkt
Wie zuvor wird die Feder wiedergegeben als Reihe von Teilchen gleicher Masse, die mit masselosen Federn gleicher Federkonstante verbunden sind.
Das obere Teilchen ist fixiert. Da eine Gravitationskraft simuliert wird, ist die Feder auf Grund des eigenen Gewichts entsprechend ausgedehnt.
Das weiße Kreuz kennzeichnet den so genannten Massenmittelpunkt der Feder, der nach einem bestimmten Verfahren von dem Programm berechnet wird.
Das isolierte Teilchen neben dem Massenmittelpunkt kann nicht fallen, da es ebenfalls fixiert ist.
Wird die Simulation gestartet und werden die Teilchen vorher gelöst, so kann man beobachten, dass der Massenmittelpunkt genau so fällt wie das frei fallenden isolierte Teilchen.>Die allgemein gültige Regel lautet:
Der Massenmittelpunkt eines materiellen Körpers bewegt sich unter dem Einfluß einer äußeren Kraft so, als ob die Masse des ausgedehnten Körpers in ihm vereinigt wäre. Innere Kräfte spielen für die Bewegung des Massenmittelpunktes keine Rolle.
Zur Benutzerschnittstelle:
Der Massenmittelpunkt aller im Kubus gesetzten Teilchen kann im Fenster "Teilchen setzen und verwalten" aktiviert werden.

Abb. 5.16.: Aktivieren der Visualisierung
des Massenmittelpunktes

Abb. 5.15.: Simulation einer fallenden Feder
mit Massenmittelpunkt

Abb. 5.16.: Aktivieren der Visualisierung
des Massenmittelpunktes
zurück zur Startseite


