9. Exercises with Satellite Orbits

9.1. Introduction

Spatial imagery is an important capability and a prerequisite to solve many different problems in physics, either in so-called ,Gedanken-experiments" or those where moving objects are involved.

The following videos and assignments are offered as some kind of exercise material, assuming that spatial imagery as any other capability can be further developed by repetitive training.

9.2. Satellite Orbits in 3d and 2d

The video Satellite Orbits in 3d and 2d shows a satellite moving around the earth while its projection perpendicular to the surface of the earth is drawn.

Once a satellite is in orbit, the orientation of the plane in which it is orbiting, is stable in space while the earth is rotating once in 24 hours around its polar axis. Therefore the projection of the satellite on the surface of the earth will look like some kind of displaced circles. The seize of the displacement will depend on the ratio of the time period for one rotation of satellite and earth.

In 3d this process looks kind of simple. The task is now to imagine, which curve will show up, if the spherical surface of the earth is represented in 2d as a rectangular map.

The video shows this transformation from 3d to 2d as a continuous process and may help to see and understand the relation between these two different representations of the identical process.

Fig 9.1.: Simulation about a polar satellite

9.3. Orbit of the ISS

In the last video the satellite was crossing over the north and south pole. The polar axis of the earth and the orbit of the satellite were therefore lying within the same plane.

The ISS - International-Space-Station - however, does not follow this orbit. There is a distinct angle between the plane of its orbit and the polar axis of the earth.

Try to imagine first, which kind of trace will occur when the position of the satellite is projected onto the 2-dimensional worldmap and play the video
Non-polar satellite to check your assumptions.

9.4. Geostationary Satellite

In general the orbit of a satellite has the form of an ellipse with the earth at one of its focus points. A special situation has been reached for the following conditions:

• The orbit of the satellite lies in the same plane as the equator of the earth.
• The orbit is not an ellipse but a circle.
• The radius of the orbit is so large that it takes 24 hours to complete one round.

The satellite under these conditions is geostationary, which means that its projection on the surface of the earth does not move but remains on the same spot.

For a computation of the radius for a geostationary satellite see the paragraph "Computation" below.

When looked at from the earth a geostationary satellite appears under a constant angle and can therefore serve for instance as transmitter of TV programs.

Look at the video ( Geostationary Satellite - A Question and try to find the answer for the posed question, before you play the next video ( Geostationary Satellite - the Answer to check your assumption .

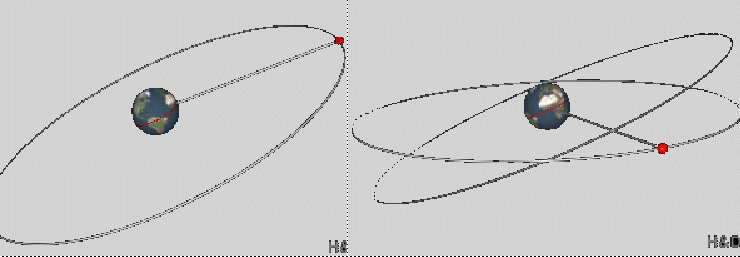
Fig 9.3.: Video about a geostationary satellite

It may be a good exercise for training spatial imagery to build a model with a globe and a satellite and to see, how this curve as projection on the surface of the globe does develop. You may also try to find out which curve will develop, if the orbit of the geostationary satellite is deformed slightly to an ellipse.

Computation of the Radius for a Geostationary Satellite

A geostationary satellite has to complete a full circle in 24 hours.

The gravitational interaction between earth and satellite has to be equal to the centripetal force needed for a circular movement. With this condition the radius R of the orbit of a geostationary satellite can be calculate as follows.

 

R ~ 4,3 10⁷ m = 43000km;
R_earth ~ 6300 km; Distance_{Earth surface - satellite} ~ 36700 km

9.5. Molniya Satellite

On the upper northern hemisphere the normal geostationary satellites are not visible. The video Molniya Satellite shows how the orbits of the so-called Molniya satellites have been selected to serve during parts of their orbit as nearly geostationary satellites.

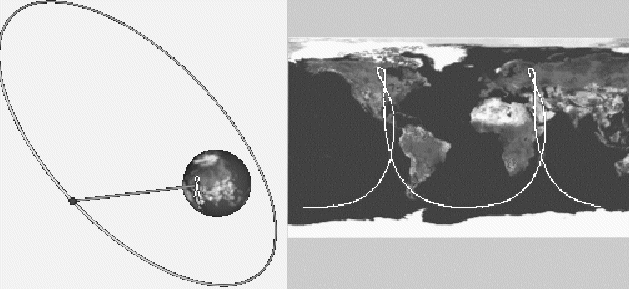
Fig 9.4.: Video about a Molniya satellite

Three of such satellites in a row are sufficient to serve for a continuous transmission.