8.1. How can a Satellite be Accelerated by a Planet?

Many times it is reported in newspapers and on TV that a satellite first passes a nearby planet to increase its speed before it is heading towards its final destination. How is this gain of momentum possible?

Why is a satellite accelerated more when it is approaching a planet than it is decelerated when it departs after the fly by?

The general law of gravity is indeed one of the most mysterious laws of nature, which is known to us. However, there is no doubt that the attractive force between two objects does not depend on the direction in space.

The Simulation "8-planet-satellite" offers the possibility to study the question posed above in detail.

In this simulation two spherical bodies (satellite and planet) are shown with a mass ratio of 1/200000. Mutual gravitation is simulated.

First case: planet at rest

In this case no gain in momentum can be expected because of the spherical symmetry of the gravitational forces. The gain in velocity, while approaching, is balanced by the lost in velocity when departing. In agreement with this statement the simulation shows, that the satellite - starting at P(0) with v(0) = 980 units - has the same speed when it has reached the point P(1) (fig 8.1).

Remark: In order to accomplish a precise measurement, the simulation can be advanced stepwise to the point P(1), at which after the fly by the same distance from the planet has been reached as at the starting point P(0).

The data for the satellite can be monitored during its fly by, by activating the monitor button in the "Particle Inspector" window"

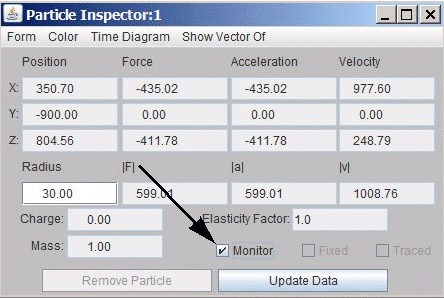
Fig 8.2.: How to activate to monitor data of a selected particle

Second case: planet is moving

The situation is changed when the planet is not at rest but moving. The direction of this movement defines a symmetry axis. Depending on its movement relative to this axis, the satellite will either speed up or slow down after having passed the planet.

Question: Assume that in the situation shown in the figure above the planet moves along the x-direction to the right. Will the planet, starting at P(0) with a distance d0 from the planet, speed up or slow down after having passed the planet and reached the same distance d1 = d0 from the planet?

When looking for an answer it may be helpful to consider that the total energy and the total momentum of the system planet/satellite must be conserved.

8.2. Conservation of Energy and Momentum

When will the satellite accelerate, when decelerate?

This question can be answered on the basis of the laws of conservation of energy and momentum.

From the law about conservation of energy it follows that the planet must slow down so that the satellite can move faster or vice versa.

To draw a conclusion from the law of conservation of momentum two cases have to be considered.

• 1. When approaching the planet the satellite moves in the opposite direction as the planet. In this case the total momentum p is smaller than the momentum of the planet.
• 2. When approaching the planet the satellite moves in the same direction as the planet. In this case the total momentum p is larger than the momentum of the planet.

For both cases it is assumed that the momentum of the planet is defined as positive.

In case 1 the total momentum of the system is being increased due to the change of direction of the satellite after having passed the planet. Conservation of momentum can only be guaranteed if the velocity of the planet is reduced accordingly. And conservation of energy implies that the velocity of the satellite must increase.

In case 2 the total momentum of the system would decrease due to the change of direction of the satellite after having passed the planet. Conservation of momentum can only be guaranteed if the velocity of the planet is increased accordingly. And this implies that the velocity of the satellite must decrease.

This rather abstract explanation can be enriched by a nore concrete once by making use of a simulation.

8.3. Acceleration of a Satellite caused by a Planet

The simulation "8-planet-satellite.acceleration" shows again two spherical objects (satellite/planet) with a mass ratio of 1/200000 and mutual gravitational attraction. The planet moves with a velocity of 100 units in the positive x-direction

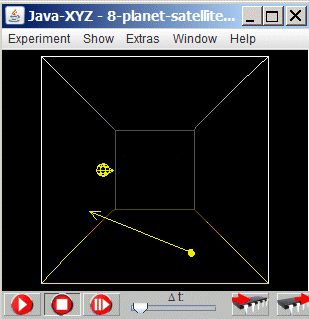
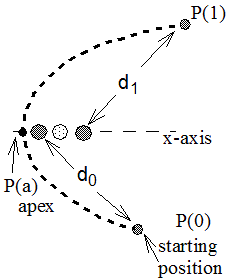
Fig 8.3.: Simulation "8-planet-satellite-acceleration"

The simulation shows that the velocity of the satellite is nearly increased by 200 units, if it has reached after fly by the point P(1) with the same distance to the satellite as at P(0).If, however, the planet moves with v = -100 units (in the negative x-direction), the velocity of the planet is decreased by nearly 200 units when having reached again the same distance to the planet as at the starting position (simulation "7-satellite-deceleration").

Remark: In order to accomplish a precise measurement, the simulation can be advanced stepwise when approaching the apex P(a) or point P(1).

Explanation

The path of the satellite when passing the planet is hyperbolic.

The simulation is set-up in such a way that this hyperbolic path is symmetrically oriented in respect to the x-axis.

When the satellite has reached the apex P(a) the distance between satellite and planet has reached a minimum. Until it has reached this point, it is approaching the planet. When it has passed this point the distance is increasing.

It follows that at the point P(a) the velocity component of the satellite in the direction of the planet - in this case the x-direction - must be the same as the velocity of the planet in the x-direction, thus nearly 100 units.

The x-component of the starting velocity of the satellite v x (0) is therefore increased by the amount (v x (0) + 100) units and this during flying time from P(0) to P(a).

For symmetry reasons we can conclude that the same velocity change will occur during the flight from P(a) to P(1) where the satellite has reached the same distance to the planet as before at P(0).

The simulation shows that the x-component at P(1) is about 200 units larger than at P(0).

By approaching stepwise the point P(a) you can check that the x-component of the satellite velocity takes the value +100 or -100 depending on the orientation of the planet velocity.

And certainly the simulation shows that the speed of the satellite is reduced, compared with the starting velocity, if the planet moves in the negativ x-direction.