back Home
7. Collision and Conservation of Momentum
Introduction
The following chapter is centred around collision processes where the term "momentum" plays an important role. The term momentum can be defined for any moving object. It is indicated as p and is defined as the product of mass m and velocity p = m v
Just as with energy there exists a law of conservation of momentum, which has universal validity.
The term "momentum", which is of high importance within classical as well as modern physics, will be introduced and explained by treating collisions processes of particles.
The video Collision of 2 spheres shows such a collision process between 2 solid metallic balls and the smooth transition to a corresponding simulation.

Fig 7.1.: Video about collision
The following simulations allow to study such collision processes in detail. Real experiments with sliders on an air cushion track or solid balls like in the video are the base of such simulations and should, if at all possible, precede or accompany any further study.
7.2. Collision with Realistic Objects
The simulation "7-collision-elastic-objects" shows a collision between two bodies, modelled as extended objects of 4 particles, interconnected by elastic springs.
As a normal result of every collision process the colliding bodies change their velocity. In addition internal vibrations are excited and the bodies may start to rotate.
Rotations and internal vibrations are phenomena which absorb energy and therefore overshadow the underlying principles. In order to detect and to understand these basic principles the collision experiments should to be designed in such a way that rotation is avoided and that the effects caused by internal vibrations can be neglected.
To avoid rotational effects head-on collisions are necessary
Fig 7.3.: Simulation "7-head-on-collision"
When the stiffness is high enough, an object can be idealized as rigid and internal vibrations can be neglected.
Nevertheless the object has to be completely elastic during the collision process. The characterization ,rigid body" therefore has to be taken as ,very very elastic but very very stiff".
The spring constant D for all existing springs can be set in the "Spring Properties" window, to be called from a submenue of the Window menue (main menue line of the JavaXYZ-cube). To apply the actual value to all existing springs, the related Button has to be activated.
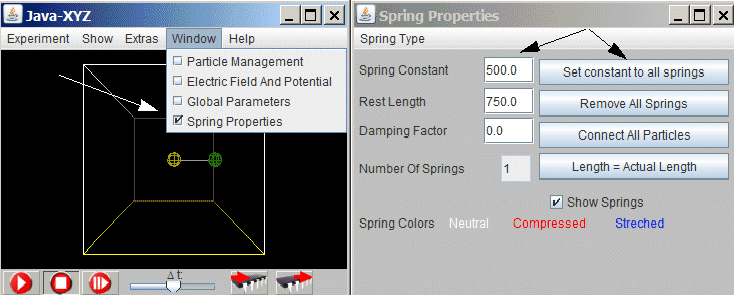
Fig 7.4.: "Spring Properties" window where a common spring constant can be applied to all existing springs
7.3 Collision with Rigid bodies - Conservation of Momentum
The mathematical treatment of collision processes is based on the model of the rigid body as an idealization, where internal vibrations can be completely neglected.
The particles in the following simulation are modelled as rigid objects. This means that the elastic deformation during collision does not use up energy and that no internal vibrations can exist.
The collisions with the walls of the cube, however, are modelled as completely inelastic. This means that during collision with the walls all energy is absorbed.
The simulation "7-collision-rigid-objects" allows to study collision processes by changing the x-component of the velocity of each particle as well as their mass.
To explain the outcome of such collision processes, two conservation laws of general validity have to be accepted: the conservation of energy and the conservation of momentum.
The derivation of these laws and the definition of energy and momentum is found in any standard textbook.
Fig 7.5.: Simulation "7-collision-rigid-objects"
Normally, when two particles collide, their velocities are changing. This implies that for every single particle its momentum (m x v) is also changing. However, it will be shown that the total momentum, the sum of both momentums, is constant in every moment in time, in other words: momentum is conserved.
In the given simulation (as mentioned above) there is an exception when a particle collides with the walls of the cube. These walls are modelled as completely inelastic and the cube as having an infinitely large mass. Therefore the cube can absorb any momentum of the particle by moving with an infinitely small velocity to the opposite side.
The following table shows the result from some collision processes to demonstrate that momentum is conserved.
To add momentum, it has to be known, that momentum is a vector.
When defined for one fixed directions, the 2 possible orientations are indicated as positive (+) or negative(-).
The total momentum of 2 particles with +p1
and -p1 is p =+p1 + -p1 = 0.
The procedure is the same as if velocities with opposite orientations have to be added.
In the following table some collision processes with different settings have been documented. More such processes can and should be entered to prove the law about conservation of momentum.
t
1
stands for a moment in time before and t
2
after collision. The numbers are given in suitable units.
Normally, when two particles collide, their velocities are changing. This implies that for every single particle its momentum (m x v) is also changing. However, it will be shown that the total momentum, the sum of both momentums, is constant in every moment in time, in other words: momentum is conserved.
In the given simulation (as mentioned above) there is an exception when a particle collides with the walls of the cube. These walls are modelled as completely inelastic and the cube as having an infinitely large mass. Therefore the cube can absorb any momentum of the particle by moving with an infinitely small velocity to the opposite side.
The following table shows the result from some collision processes to demonstrate that momentum is conserved.
To add momentum, it has to be known, that momentum is a vector.
When defined for one fixed directions, the 2 possible orientations are indicated as positive (+) or negative(-).
The total momentum of 2 particles with +p1
and -p1 is p =+p1 + -p1 = 0.
The procedure is the same as if velocities with opposite orientations have to be added.
In the following table some collision processes with different settings have been documented. More such processes can and should be entered to prove the law about conservation of momentum.
t 1 stands for a moment in time before and t 2 after collision. The numbers are given in suitable units.


