5.1. Fall and Throw - Law of Gravitation

Weight - Weightlessness

In the middle of the 17. century Newton formulated the universal law of gravity, stating that all material objects are interacting in the form of mutual attraction (see section 5.2.).

Due to the gravitational interaction with the total mass of the earth, every material object has weight. But what about weightless conditions? Does the child in the figure has weight or is it without weight? Only in this very moment or during the complete "throw"? These questions and others related to movements under the influence of gravity will be answered on the following pages

Fig. 5.1.: Is this child weightless?

5.2. Law of Gravity

Qualitative Description

The phenomenon of gravitation means that all material objects attract each other. Because of this fact all objects are attracted by the earth and have therefore weight. This seems to be a rather normal fact, however, until today the physicists have not found any explanation for it. It must be accepted as a basic phenomenon which cannot be explained or reduced to a more basic principle.

The attracting force between two material objects 1 and 2 is proportional to a specific property of these objects, which me call here tentatively grav-property.

It has been shown experimentally that under all circumstance this grav-property is proportional to the former introduced term "mass". This fact is at first sight rather astonishing, because there is no obvious relation between the property of an object to resist acceleration - its inertial mass - and the property to attract another material object.

Einstein has developed an explanation in his General Theory of Relativity, which involves curved spaces and which can only be understood by specialists. There are other more speculative explanation, where inertia is reduced to a special gravitational effect, involving the galaxies of the whole cosmos.

In any case it is now generally accepted that the strict proportionality of inertial mass and the above introduced grav-property indicates, that both have a common origin. Therefore both properties are nowadays called "mass". To distinguish between these two properties, they are often called "inertial mass" m_s and "gravitational mass" m_g .

Quantitative Description

A universal law can be stated: all material objects attract each other.

The attracting force between two material objects 1 and 2 is proportional to m ₁ and proportional to m ₂. The attracting force also depends on the distance r between the attracting objects. Its magnitude is inversely proportional to the square of the distance between the centres of the two bodies.

Quantitatively, the gravitational law can be written as:

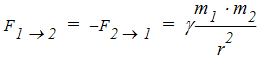
The constant γ is a universal constant of nature.

5.3. Objects in Free Fall

All objects - when starting from rest - fall to the ground with the same, constantly increasing velocity, independent of their weight (if air resistance is neglected). The video ,Free Fall" shows an experiment where three different ball of quite different weight are dropped from a height of about 4m.

Fig 5.2.: Video about an experiment where 3 objects
of different weight drop down (Falling objects)

For many people this may not be an astonishing fact because they take this as a law of nature. There are, however, many people who are convinced that smaller and lighter objects are dropping slower than larger and heavier ones. There is an astonishing point here.

A smaller object is pulled downwards by the earth with a smaller force than a larger object made from the same material. Why will nevertheless both objects fall along equal distances in equal length of time?

The answer is found in the fact that the object with a smaller gravitational mass has also a smaller inertial mass. Therefore its resistance against acceleration is less. And since gravitational mass and inertial mass are strictly proportional, these two effects - less attracting force and less inertia - cancel for every object and every amount of mass. The prepared simulation "5-free-fall" demonstrates that the program JavaXYZ is in agreement with reality. This is of course not astonishing. Astonishing is the fact that inertial mass and gravitational mass are proportional

Fig 5.3.:Simulation "5-free-fall"

5.4. Drop Distance and Drop Time

All objects experience the same acceleration when dropping down to earth. This implies that a general relation exists to determine the drop distance from a given drop time which is valid for all objects, independent of their weight.

For the simple case that an objects is released from rest this relation reads:

s = 1/2 g t^2;

s = drop distance ; g = acceleration due to gravity; t = drop time

The simulation "5-free-fall-2" explains, how this relation can be derived. In this simulation an electric field is applied in negative z-direction (downwards) but no gravitational field exists. Since the right particle is charged, it moves under a constant force and therefore with a constant acceleration a c. The left neutral particle moves due to its starting velocity with constant speed vc. Question: What constant velocity vc is necessary for the body on the left so that both reach the bottom of the cube at the same moment in time?

Fig 5.4.: Comparison of 2 objects moving with
constant speed and constant acceleration
Simulation "5-free-fall-2"

The starting velocity of the left particle can be changed in the "Particle Inspector" window.

Result:

The velocity of the accelerated body increases from zero to a maximum value v_max when it hits the bottom of the cube.

To cover the same distance s_max during the same time the body on the left must move with a constant velocity v = v_max /2. With this starting velocity it is too fast at the beginning and too slow at the end. Since the velocity of the accelerated body does increase linearly from zero up to v_max, this "too slow" and "too fast" will balance and both objects will reach the bottom at the same motment in time

The body on the left, moving with constant velocity covers during the time period t_max the distance: .

For a constant acceleration we get for the velocity as function of time v_max = g t_max.

For the distance s_max we get:

This relation is valid for arbitrary distances and time spans as long as the object starts from rest. Therefore the index can be removed and we get as relation between distance to fall and time to fall:

The simulation "5-free-fall" with the parameters: s _{max = 2000 units; g = 10 units shows an agreement between the mathematical relation given above (with v = v max /2 )}

5.5 Free of Weight and Free of Force - An Important Difference

When looking at astronauts as they are floating in their space craft while circulating around the earth, it is obvious that they are weightless. But are they also free of force? Certainly not, because these space crafts move within the gravitational field of the earth. For usual orbits the strength of this field is nearly the same as here on earth.

The same is valid for an object in free fall. It certainly is weightless, otherwise scientists would not have build a so-called drop tower at University Bremen, Germany, where low-cost experiments under conditions of weightlessness are carried out.

Look at the video and try to find the answer to the question posed about a throw upwards.

Fig 5.5.: Video about the drop-tower at Bremen
Droptower at Bremen (Germany)

Explanation (Free of weight - Free of force)

An object has weight when it is in equilibrium between two forces, gravity pulling downward and a counter force, applied by the ground, pushing upward.

A scale indicates as weight either this force downward or this counter force which is necessary to keep up the equilibrium.

Due to these two forces, oriented downward and upward, an object will be more or less deformed depending on its elasticity. This elastic deformation disappears when there is no counter force from the ground but when only the gravitational force oriented downward is applied.

Gravity applies to every single atom or molecule of any object in the same manner and therefore does not created any tension or elastic deformation. It is this non-deformed state which is interesting for scientist. Therefore such experiments under weightless conditions are carried out, either in a drop tower or in space crafts like the ISS.

Why objects in space crafts are weightless will be explained in later chapters.

5.6. Vertical Throw Upward

Starting Velocity and Time to Rise

The prepared simulation "5-vertical-throw" allows to find out which starting velocity upward is necessary for the ball to move against gravity and to reach the top of the cube without bouncing against it. Simulated is a constant gravitational field downwards.

Such a gravitational field can be activated in the Global Parameter window.

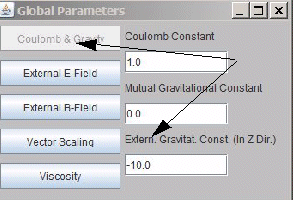
Fig 5.6.: Simulation "5-vertical-throw"
How to set and change an external gravitational field in z-direction

A vertical throw and a vertical fall are symmetric movements with constant acceleration.

Therefore the same equations have to be applied.

s = 1/2 g t2; v = g t + v ₀

In the simulation the value for the acceleration is g = -10 units.

Is there an agreement between the results of the simulation and these equations?

5.7. Horizontal Throw

The Experiment and a Question

The video Horizontal Throw shows an experiment, where a ball is pushed horizontally from a height of about 4 m and hits a basket full of water at a distance of about 6 m.

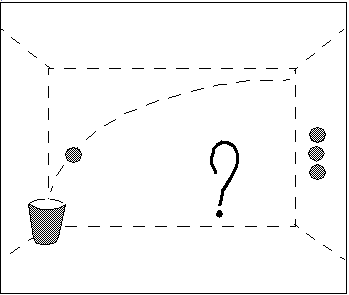
Fig 5.7.: Video about a horizontal throw

Question:

If a second ball would start to fall vertically at the same moment in time when the ball is pushed horizontally, would it reach the floor before or later or at the same moment in time?

A first answer can be found by using the prepared simulation "5-horizontal-throw" (next chapter) .

Principle of Superposition

It would not be a simple task to set up a real experiment where the two balls are released at the same moment in time with variable or no horizontal velocity components. To develop a corresponding simulation is rather simple and is sufficient, because of a basic principle - the so-called superposition principle. This principle is based on the fact that a force has absolutely no influence in a direction perpendicular to its own direction.

In our case this means that gravity cannot change the horizontal velocity component in any way. This component of the velocity remains constant - it will at least not be influenced by gravity - while the acceleration downward will be the same as for all free falling objects. The two balls will therefore - as demonstrated by the simulation - always hit the ground at the same moment in time. This will happen in any real experiment with an accurate experimental setup. You may find out by trial and error, that a specific velocity v0 is the right one to hit the ball on the left.

Fig 5.8.: Simulation "5-horizontal-throw"
(with a simulated gravitational field downwards)

The simulation indicates in accordance with reality that the movement of the horizontal throw is an independent superposition of a horizontal component with constant velocity and a vertical component with constant acceleration.

An alternative to trial and error is an approach based on theory as shown below.

Numerical Solution

In the video the question was posed; What starting velocity is needed for the ball to hit the basked (distance 8m) from a height of 5m?

To answer this question, the following relations are needed and have to be understood:

For a movement with constant acceleration: s = 1/2 g t²; v = a t; (if started at rest).
(s = distance travelled; v = velocity; g = acceleration; t = time span)

For a movement with constant velocity: s = v t.

From the principle of superposition it follows that the movement shown in the video and by the simulation can be separated in two parts, a free fall with constant acceleration a = g and a horizontal movement with constant velocity v.
For the free fall in perpendicular direction we have:

For the horizontal movement we have: The values for the simulation are: s1= 1800 units; s2 = 1800 units; g = -100 units. Is there an agreement between theory and simulation?

5.8.Inclined Throw

The Experiment

The inclined rod, seen in the video, is hold under tension by two strong springs. When released, the top of the rod hits the ball and after quite a few tryouts with different starting positions and different inclinations the ball reached the basket and made a point.

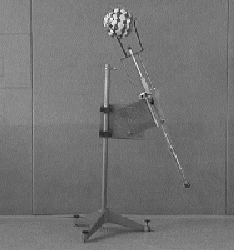
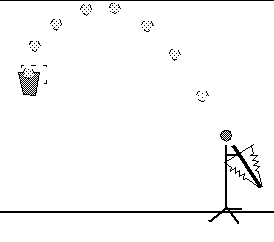
Fig 5.9.:Inclined Throw (see Video Inclined throw)

The next simulation repeats this experiment, followed by a numerical solution.

The Simulation

By changing the horizontal and vertical components of the starting velocity (see fig.3.1) you may try to hit the "basket" but as much as possible from above, without hitting the "ceiling". An alternative to trial and error is an approach based on theory.

Fig 5.10.: Simulation 5-inclined-throw

Numerical solution:

To solve numerically the problem posed in the video, the following relations are needed and have to be understood:

• For a movement with constant acceleration a _c : s = 1/2 g t² ; v = g t;
  (s = distance travelled; v = velocity; g = acceleration due to gravity; t = time span)
• For a movement with constant velocity v_c : s = v t.

From the principle of superposition it follows that the movement shown in the video and by the simulation can be separated in two parts, a vertical throw with constant acceleration and a horizontal movement with constant velocity.

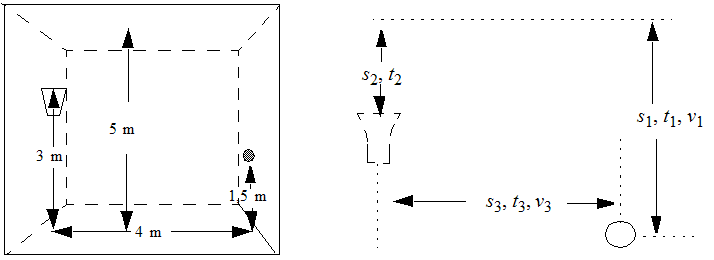
For the two parts of the vertical throw with velocity upward and downward we have:

For the horizontal movement we have:

The values for the simulation are:
s₁ = 1250 units; s₂ = 450 units; s₃ = 1600 units; g = -100 units.

Is there an agreement between theory and simulation?

5.9. A Long Stick and a Ball Dropping Down - Which One is First?

It has been shown that all objects experience the same acceleration when dropping down to the earth. If confronted with an experimental setup as seen in the following video, you may at first sight assume that the stick and the ball, when released simultaneously, will hit the ground at the same moment in time.

Fig 5.11.: Video about a dropping stick and a ball
(A dropping stick and a ball

Are you astonished when you observe the outcome of this experiment? (look at the video Falling stick and ball - the experiment

The puzzling question is: What is the extra force (in addition to gravity), which causes the upper end of the stick to accelerate more than the free falling ball?

Stick and Ball (Explanation)

A first answer is a rather simple one. In this experiment two different cases are compared. The ball is under the influence of gravity only and therefore it is in free fall. The inclined stick, however, is not only under the influence of gravity but is also in interaction with the floor. It is therefore not in free fall and so we should not expect a simple result.

By experimenting with the prepared experiment ,Stick and Ball" you can learn more about the processes related with this experiment.

Stick and Ball (Simulation)

Similar to the video the simulation "5-falling-stick-ball" allows to compare the free fall of a ball and the movement of an inclined stick. The stick is modelled by single particles, connected by elastic springs.

Fig 5.12.: A falling stick and a falling ball
(simulation "5-falling-stick-ball")

While the left corner of the stick is fixed, the other parts are forced to move on more or less circular paths around this fixed point.

Due to the two forces, gravity and the reaction from the floor, the stick is bending and increasing elastic forces lead to increased acceleration.

If the elasticity is reduced by applying more springs, (simulation "5-falling-stiff-stick-ball") the bending is nearly invisible.

The stiffer the stick the better the agreement between the experiment and what is shown in the simulation.

5.10. A "Slinky" dropping down

Assume that your neighbour upstairs is bending out of his window and holds the upper end of a rather soft spring, a so-called Slinky, in his hand. The Slinky expends under gravity and ends up in front of your window, where you only see the lower end of the spring.

Fig 5.13.: Video about a falling Slinky
A falling elastic spring (Slinky)

The question is: What will happen to this lower end, when your neighbour releases the spring? Will it move upwards a little, will it stay for a short while before starting to drop or will it immediately start dropping?

Look at the video indicated in fig.5.12 and make up your mind about the question posed.

If you look carefully at the next video (A falling Slinky - the experiment), which shows the experiment, you can detect that the lower end of the Slinky does not start immediately but only when the spring has nearly collapsed.

This process can be studied in slow motion with the simulation "5-falling-slinky"

Simulation " 5-falling-slinky"

In this simulation a Slinky is modelled as a sequence of particles of equal mass connected by short elastic springs of equal spring constant. The particle on top is fixed.

Fig 5.14.: Simulation of a falling slinky

Since gravity is active the spring is expended under its own weight. The single particle next to the lower end of the Slinky does not fall because it is fixed.

If you start the simulation and release the fixed particles before, you can observe when the lower particle starts falling.

To fix or to release a particle can be controlled inside the "Partlicle Inspector"window

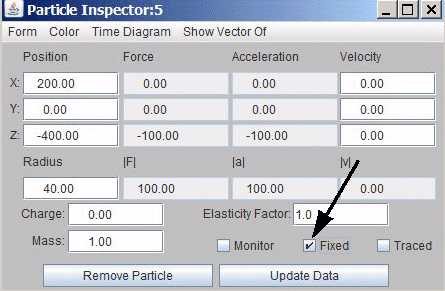
Fig 5.15.: How to fix or release a particle

Result:

The lower particle cannot start to fall immediately because the spring has not yet collapsed and therefore compensates gravity.

5.11. Centre of Mass - an Important Concept

With the following simulation the concept of "Centre of Mass" (CoM) is introduced. This concept will not be derived from more basic principles but is just demonstrated to show its unique property and to motivate for more extended study.

In the simulation "5-centre-of-mass" the Slinky is modelled as before as a sequence of particles of equal mass connected by short elastic springs of equal spring constant.

Fig 5.16.: Simulation "5-centre-of-mass"

The particle on top is fixed. Since gravity is active all the springs are expended under the weight of the particles.

The white cross in this simulation indicates the so-called centre of mass of the Slinky.

The single particle next to the centre of mass of the Slinky does not fall because it is fixed.
If you start the simulation and release before the fixed particles (fig. 5.11), you can observe that the centre of mass moves exactly at the same pace as the free falling body.

The general rule is:

The centre of mass of an extended material object behaves under the influence of an external force as if all the mass of the extended object is concentrated at this point. Internal forces have no influence on its movement.

The centre of mass of all particles placed inside the cube can be visualized inside the "Particle Mamagement" window