back to Home
4 Concept of Force
4.1. General Properties
In physics the concept of force is used since Newton to understand and describe mechanical processes.
A so-called Newtonian force as it is understood in physics has the following properties:
-
A force is the cause of change, either of the movement of an object or of its form or volume.
-
A force is always the result of an interaction between at least two objects. This implies that a force can never exist on its own, it always appears in pairs. These two paired forces have always the same strength and direction but opposite orientation.
-
A force has a unique direction with two possible orientations, usually indicated as positive or negative.
-
A force has a point of attack or point of application.
4.2.Force as Vector
Every force as a term in physics has two different properties: an amount and a direction.
A term with these two properties is called a "vector".
Such a vector is represented and visualized as arrow
4.3. Force and Acceleration
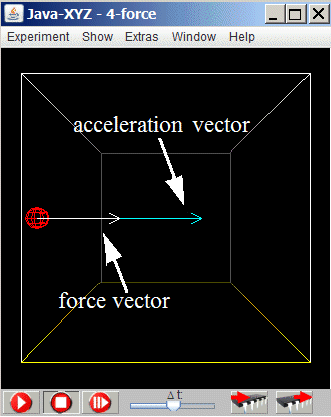
Fig 4.1.: Simulation "4-force";
movement with constant acceleration
The prepared simulation "4-force" demonstrates the effect of a force on the movement of a particle.
As in the previous simulation the force is simulated by setting the charge of the particle to a positive value (in the Particle Inspector window) and giving the strength of an electric field (in the positive direction of the x-axis) a positive value (in the Global Parameters window).
The arrows indicate the directions and amounts of the applied force f (white) and the resulting acceleration a (blue). The latter two values are indicated numerically in the "Particle Inspector" window.
By changing the mass of the particle (in the "Particle Inspector" window) the simulation shows that the acceleration a and the mass m are inverse proportional. If you double the mass, the acceleration is divided in halve and vice versa. This relation is valid in general and should be intuitively clear: the more mass an object has, the slower can it be set in motion, assuming a constant force. Such an inverse relation implies, that the product of mass and acceleration is constant.
More to this relation will be found in the next chapter.
4.4. Newtonian Force, Inertia and Mach´s Principle
Newton`s 2nd Law
In the former chapter it has been stated, that under the influence of a constant force the product of mass m and acceleration a of a moving object is constant.
This relation - the inverse proportionality of m and a - has been tested experimentally and has been found to be valid under all circumstances, at least unless not very high velocities (comparable with the speed of light) get involved.
This product - m x a - has been taken as definition and as a measure for the strength of a force which leads to the famous equation, set up in the 17. century by Isaac Newton:
F = m x a (m = mass ; a = acceleration
 In practical all physics textbooks, a situation according to this equation is visualized by a single vector F applied to an object with a mass m.
In practical all physics textbooks, a situation according to this equation is visualized by a single vector F applied to an object with a mass m.
Inertia
From experience in daily life we know that an object resists, if we try to make it move faster or if we want to reduce its speed.
In traditional physics this resistance is called inertia and is seen as a property of matter. And as a property of matter, it cannot be a Newtonian force. An important and indispensable character of a Newtonian force is that is has to occur as interaction between two objects. It cannot be the property of a single object. Furthermore inertia can never accelerate an objects. It can only react on acceleration.
And since such an interactive partner is missing, the resistance of a material object against any kind of acceleration is not seen as a force and is not visualized as such in traditional textbooks.
Mach´s Principle
There is an exception, which dates back to the beginning of the 20 century. At that time, the German physicist Mach proclaimed some principles about general relativity and published the idea that the presence of the matter of all the galaxies in the universe is responsible for the inertial mass of objects here on earth.
The broad notion is that "mass there influences inertia here".
Until today this idea has never been experimentally approved or disproved and therefore remains speculative. However it opens the possibility to think of a possible interactive partner for inertia and facilitates to accept the resistance of a material object against acceleration as a real force.
In the following learning material the possibility is offered to accept this idea of inertia as a real force and to visualized it, when ever wanted, as follows.
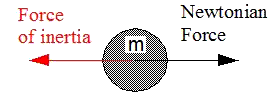
Fig 4.2.: Visualization of a Newtonian force and the equal
and oppositely oriented force of inertia as an acceleration-reaction-force
By doing so it has to be kept in mind that a force of inertia, even though it is real, is not a Newtonian force, which can be applied to accelerate an object. The force of inertia is an acceleration-reaction force, which only exists during the process of acceleration. It cannot be applied to an object to cause acceleration. But if a Newtonian force is applied to an object this force of inertia makes acceleration possible by producing the necessary resistance.
Without it the Newtonian force would act against something without resistance, it would pull or push against nothing or emptiness. It seems reasonable to claim that this could have no effect.
The following simulations demonstrates different kinds of accelerated movements and allows the user to visualize independently the Newtonian as well as the forces of inertia.
4.5. Force of Inertia
With the idea of inertia as an acceleration-reaction force the dynamic situation, where an object is accelerated by a Newtonian force can be described as an equilibrium between two forces, a Newtonian force and a force of inertia - an acceleration-reaction force.
Both forces can be visualized independently as vectors.
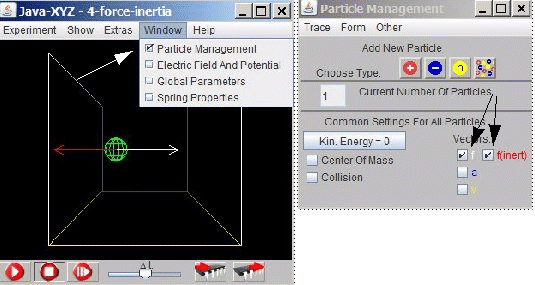
Fig 4.3.: Simulation "4-force-inertia". How to visualize a Newtonian and
an inertial force common for all particle to be set
The "Particle Inspector" window offers the possibility to visualize these forces for an individual particle.
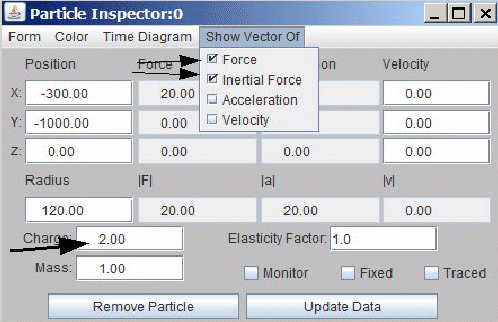
Fig 4.4.: How to visualize a Newtonian and an inertial force
(an acceleration-reaction force) for a selected particle
An accelerated movement can now be described as if there exists always an equilibrium between an applied Newtonian force and a force of inertia as acceleration-reaction force. This description of a movement is valid for all objects independent a of their mass.
The accordance of the simulation with this last statement can be checked by changing either the mass of the particle or the strength of the applied force by changing the charge of the selected particle(in the "Particle Inspector" window).
Mathematical description
With the idea of inertia as an acceleration-reaction force, the movement of an object being accelerated by an applied Newtonian force can be interpreted as an equilibrium and represented in mathematical form as:
FNewton = - FInertia
Since we have FNewton = m a (Newton´s Principles, law II)
it follows:
FInertia = - m a;
The equation FNewton = - FInertia
is an expression for equilibrium and should not be identified with a static or stationary situation where two Newtonian forces are applied to the same object. In such a case, the sum of all applied Newtonian forces is zero and the object will remain in its state of rest, or uniform motion in a straight line (Newton´s Principles, law I).
An equilibrium between a Newtonian and an acceleration-reaction-force, a force due to inertia, does only exist during the process of acceleration.
With the idea of inertia as an acceleration-reaction force, the rule to be learned is rather simple:
There exists always an equilibrium between two forces, either in a static or stationary situation between two Newtonian forces or during acceleration between a Newtonian force and a force of inertia.
4.6. Elastic Interaction and Force of Inertia
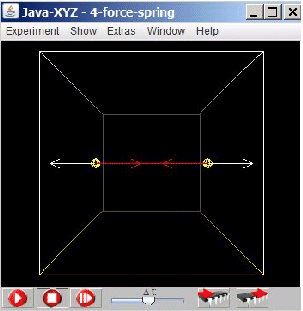
Fig 4.5.: Simulation 4-force-spring
The simulation "4-force-spring" shows the movement of two objects connected by an elastic spring. Again it is possible to visualize the equilibrium between the Newtonian forces, exerted by the spring and the inertial forces as acceleration-reaction force.
A compressed spring is indicated as a red line, an extended spring as a blue line. A neutral spring is indicated as white line.
The simulation shows in accordance with reality that in every moment the inertial force Finert
is of equal strength as the Newtonian force
FN, applied by the spring. Both forces act in the same direction but with opposite orientation. FN = - Finert
A spring can be set between two particles by 1. keeping the shift-key down and 2. by selecting one particle with the left mouse button down and release the button on top of the other particle. If this procedure is repeated over an existing spring, the "Spring Editor" window opens, where spring parameters can be set.
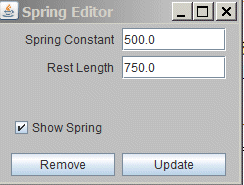
Fig 4.6.: Spring Editor window
Since the visualization of the force of inertia can be suppressed, it is always possible to explain Newton´s law with inertia as a property of mass in the traditional way.
The simulation above can be used to find out, what will happen if the mass of both particle will be changed. The mass of a particle can be changed inside the "Particle Inspector" window. An explanation for the demonstrated effect is given in the next chapter.
4.7. Elastic Interaction - Hook´s Law
A spring at rest without any applied force has a certain length l0.
When equal forces are applied at both ends the spring will either extend or shorten and change its length to l.
Due to this change of length the spring will react with a force of elastic origin Felastic
which is (within limits) proportional to 2 terms:
- the difference between l and l0.
- a spring constant D which is specific for every spring and indicates how stiff or soft a spring is. The larger D the stiffer the spring.
These relations are represented in mathematical form as:
Felastic = s D (l - l0 = s).
This law is called "Hook´s law".
During the process of acceleration the length s and therefore also the force F are not constant but are changing in time.
The direction of the force is such that both particles will always be accelerated towards the position of rest, when the spring is without tension.
The larger the mass m of the particles the smaller is the acceleration due to the force of the spring (not depending on the mass of the particles).
As a result of an increased mass of the oscillating objects the oscillation will need more time for one cycle.
4.8. Force and Constant Velocity
If an object moves with constant velocity many people believe that it needs a constant driving force to keep the velocity constant. If for instance car drivers want to increase the speed of their car they have to increase the driving force of the motor by stepping on the gas pedal or have to lift their foot to slow down.
So the conclusion is: To keep up a movement with constant velocity, it needs a constant driving force.
This conclusion implies: If there is no driving force, the object will come to rest.
From a physics perspective these conclusions are problematic, because they are in contradiction to one a the basic laws in Mechanics - Newton´s 2nd principle - stating that a constant force will cause a constant acceleration, a linearly increasing or decreasing velocity, depending on the orientation of the force
A series of videos have been developed which shows scenes from daily life, where objects are shown, moving with constant speed.
Vehicle on a country road
Gliding aeroplane
Ship in calm water
Motor boat on a river
Skydiver on an open parachute
A balloon floating in the wind
Bubbles raising in a liquid
Slider on an air-cushion track
The message of each of these videos is the same: If the sum of all applied forces cancel each other, so that the sum of all forces is zero, the object will move with constant speed.
zurück zur Startseite
4.3. Force and Acceleration

Fig 4.1.: Simulation "4-force";
movement with constant acceleration
The prepared simulation "4-force" demonstrates the effect of a force on the movement of a particle.
As in the previous simulation the force is simulated by setting the charge of the particle to a positive value (in the Particle Inspector window) and giving the strength of an electric field (in the positive direction of the x-axis) a positive value (in the Global Parameters window).
The arrows indicate the directions and amounts of the applied force f (white) and the resulting acceleration a (blue). The latter two values are indicated numerically in the "Particle Inspector" window.
By changing the mass of the particle (in the "Particle Inspector" window) the simulation shows that the acceleration a and the mass m are inverse proportional. If you double the mass, the acceleration is divided in halve and vice versa. This relation is valid in general and should be intuitively clear: the more mass an object has, the slower can it be set in motion, assuming a constant force. Such an inverse relation implies, that the product of mass and acceleration is constant.
More to this relation will be found in the next chapter.

Fig 4.1.: Simulation "4-force";
movement with constant acceleration
4.4. Newtonian Force, Inertia and Mach´s Principle
Newton`s 2nd Law
In the former chapter it has been stated, that under the influence of a constant force the product of mass m and acceleration a of a moving object is constant.
This relation - the inverse proportionality of m and a - has been tested experimentally and has been found to be valid under all circumstances, at least unless not very high velocities (comparable with the speed of light) get involved.
This product - m x a - has been taken as definition and as a measure for the strength of a force which leads to the famous equation, set up in the 17. century by Isaac Newton:
F = m x a (m = mass ; a = acceleration
 In practical all physics textbooks, a situation according to this equation is visualized by a single vector F applied to an object with a mass m.
In practical all physics textbooks, a situation according to this equation is visualized by a single vector F applied to an object with a mass m.
Inertia
From experience in daily life we know that an object resists, if we try to make it move faster or if we want to reduce its speed.
In traditional physics this resistance is called inertia and is seen as a property of matter. And as a property of matter, it cannot be a Newtonian force. An important and indispensable character of a Newtonian force is that is has to occur as interaction between two objects. It cannot be the property of a single object. Furthermore inertia can never accelerate an objects. It can only react on acceleration.
And since such an interactive partner is missing, the resistance of a material object against any kind of acceleration is not seen as a force and is not visualized as such in traditional textbooks.
Mach´s Principle
There is an exception, which dates back to the beginning of the 20 century. At that time, the German physicist Mach proclaimed some principles about general relativity and published the idea that the presence of the matter of all the galaxies in the universe is responsible for the inertial mass of objects here on earth.
The broad notion is that "mass there influences inertia here".
Until today this idea has never been experimentally approved or disproved and therefore remains speculative. However it opens the possibility to think of a possible interactive partner for inertia and facilitates to accept the resistance of a material object against acceleration as a real force.
In the following learning material the possibility is offered to accept this idea of inertia as a real force and to visualized it, when ever wanted, as follows.
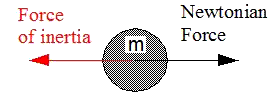
Fig 4.2.: Visualization of a Newtonian force and the equal
and oppositely oriented force of inertia as an acceleration-reaction-force
By doing so it has to be kept in mind that a force of inertia, even though it is real, is not a Newtonian force, which can be applied to accelerate an object. The force of inertia is an acceleration-reaction force, which only exists during the process of acceleration. It cannot be applied to an object to cause acceleration. But if a Newtonian force is applied to an object this force of inertia makes acceleration possible by producing the necessary resistance.
Without it the Newtonian force would act against something without resistance, it would pull or push against nothing or emptiness. It seems reasonable to claim that this could have no effect.
The following simulations demonstrates different kinds of accelerated movements and allows the user to visualize independently the Newtonian as well as the forces of inertia.
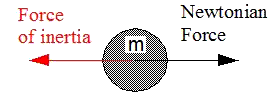
Fig 4.2.: Visualization of a Newtonian force and the equal
and oppositely oriented force of inertia as an acceleration-reaction-force
4.5. Force of Inertia
With the idea of inertia as an acceleration-reaction force the dynamic situation, where an object is accelerated by a Newtonian force can be described as an equilibrium between two forces, a Newtonian force and a force of inertia - an acceleration-reaction force.
Both forces can be visualized independently as vectors.

Fig 4.3.: Simulation "4-force-inertia". How to visualize a Newtonian and
an inertial force common for all particle to be set
The "Particle Inspector" window offers the possibility to visualize these forces for an individual particle.

Fig 4.4.: How to visualize a Newtonian and an inertial force
(an acceleration-reaction force) for a selected particle
An accelerated movement can now be described as if there exists always an equilibrium between an applied Newtonian force and a force of inertia as acceleration-reaction force. This description of a movement is valid for all objects independent a of their mass.
The accordance of the simulation with this last statement can be checked by changing either the mass of the particle or the strength of the applied force by changing the charge of the selected particle(in the "Particle Inspector" window).

Fig 4.3.: Simulation "4-force-inertia". How to visualize a Newtonian and
an inertial force common for all particle to be set

Fig 4.4.: How to visualize a Newtonian and an inertial force
(an acceleration-reaction force) for a selected particle
Mathematical description
With the idea of inertia as an acceleration-reaction force, the movement of an object being accelerated by an applied Newtonian force can be interpreted as an equilibrium and represented in mathematical form as:
FNewton = - FInertia
Since we have FNewton = m a (Newton´s Principles, law II)
it follows:
FInertia = - m a;
The equation FNewton = - FInertia
is an expression for equilibrium and should not be identified with a static or stationary situation where two Newtonian forces are applied to the same object. In such a case, the sum of all applied Newtonian forces is zero and the object will remain in its state of rest, or uniform motion in a straight line (Newton´s Principles, law I).
An equilibrium between a Newtonian and an acceleration-reaction-force, a force due to inertia, does only exist during the process of acceleration.
With the idea of inertia as an acceleration-reaction force, the rule to be learned is rather simple:
There exists always an equilibrium between two forces, either in a static or stationary situation between two Newtonian forces or during acceleration between a Newtonian force and a force of inertia.
4.6. Elastic Interaction and Force of Inertia

Fig 4.5.: Simulation 4-force-spring
The simulation "4-force-spring" shows the movement of two objects connected by an elastic spring. Again it is possible to visualize the equilibrium between the Newtonian forces, exerted by the spring and the inertial forces as acceleration-reaction force.
A compressed spring is indicated as a red line, an extended spring as a blue line. A neutral spring is indicated as white line.
The simulation shows in accordance with reality that in every moment the inertial force Finert
is of equal strength as the Newtonian force
FN, applied by the spring. Both forces act in the same direction but with opposite orientation. FN = - Finert
A spring can be set between two particles by 1. keeping the shift-key down and 2. by selecting one particle with the left mouse button down and release the button on top of the other particle. If this procedure is repeated over an existing spring, the "Spring Editor" window opens, where spring parameters can be set.

Fig 4.6.: Spring Editor window
Since the visualization of the force of inertia can be suppressed, it is always possible to explain Newton´s law with inertia as a property of mass in the traditional way.
The simulation above can be used to find out, what will happen if the mass of both particle will be changed. The mass of a particle can be changed inside the "Particle Inspector" window. An explanation for the demonstrated effect is given in the next chapter.
4.7. Elastic Interaction - Hook´s Law
A spring at rest without any applied force has a certain length l0.
When equal forces are applied at both ends the spring will either extend or shorten and change its length to l.
Due to this change of length the spring will react with a force of elastic origin Felastic
which is (within limits) proportional to 2 terms:
- the difference between l and l0.
- a spring constant D which is specific for every spring and indicates how stiff or soft a spring is. The larger D the stiffer the spring.
These relations are represented in mathematical form as:
Felastic = s D (l - l0 = s).
This law is called "Hook´s law".
During the process of acceleration the length s and therefore also the force F are not constant but are changing in time.
The direction of the force is such that both particles will always be accelerated towards the position of rest, when the spring is without tension.
The larger the mass m of the particles the smaller is the acceleration due to the force of the spring (not depending on the mass of the particles).
As a result of an increased mass of the oscillating objects the oscillation will need more time for one cycle.
4.8. Force and Constant Velocity
If an object moves with constant velocity many people believe that it needs a constant driving force to keep the velocity constant. If for instance car drivers want to increase the speed of their car they have to increase the driving force of the motor by stepping on the gas pedal or have to lift their foot to slow down.
So the conclusion is: To keep up a movement with constant velocity, it needs a constant driving force.
This conclusion implies: If there is no driving force, the object will come to rest.
From a physics perspective these conclusions are problematic, because they are in contradiction to one a the basic laws in Mechanics - Newton´s 2nd principle - stating that a constant force will cause a constant acceleration, a linearly increasing or decreasing velocity, depending on the orientation of the force
A series of videos have been developed which shows scenes from daily life, where objects are shown, moving with constant speed.
Vehicle on a country road
Gliding aeroplane
Ship in calm water
Motor boat on a river
Skydiver on an open parachute
A balloon floating in the wind
Bubbles raising in a liquid
Slider on an air-cushion track
The message of each of these videos is the same: If the sum of all applied forces cancel each other, so that the sum of all forces is zero, the object will move with constant speed.
zurück zur Startseite

Fig 4.5.: Simulation 4-force-spring
A compressed spring is indicated as a red line, an extended spring as a blue line. A neutral spring is indicated as white line.
The simulation shows in accordance with reality that in every moment the inertial force Finert is of equal strength as the Newtonian force FN, applied by the spring. Both forces act in the same direction but with opposite orientation. FN = - Finert
A spring can be set between two particles by 1. keeping the shift-key down and 2. by selecting one particle with the left mouse button down and release the button on top of the other particle. If this procedure is repeated over an existing spring, the "Spring Editor" window opens, where spring parameters can be set.

Fig 4.6.: Spring Editor window
The simulation above can be used to find out, what will happen if the mass of both particle will be changed. The mass of a particle can be changed inside the "Particle Inspector" window. An explanation for the demonstrated effect is given in the next chapter.
When equal forces are applied at both ends the spring will either extend or shorten and change its length to l.
Due to this change of length the spring will react with a force of elastic origin Felastic which is (within limits) proportional to 2 terms:
- the difference between l and l0.
- a spring constant D which is specific for every spring and indicates how stiff or soft a spring is. The larger D the stiffer the spring.
Felastic = s D (l - l0 = s).
This law is called "Hook´s law".
During the process of acceleration the length s and therefore also the force F are not constant but are changing in time.
The direction of the force is such that both particles will always be accelerated towards the position of rest, when the spring is without tension.
The larger the mass m of the particles the smaller is the acceleration due to the force of the spring (not depending on the mass of the particles).
As a result of an increased mass of the oscillating objects the oscillation will need more time for one cycle.
So the conclusion is: To keep up a movement with constant velocity, it needs a constant driving force.
This conclusion implies: If there is no driving force, the object will come to rest.
From a physics perspective these conclusions are problematic, because they are in contradiction to one a the basic laws in Mechanics - Newton´s 2nd principle - stating that a constant force will cause a constant acceleration, a linearly increasing or decreasing velocity, depending on the orientation of the force
A series of videos have been developed which shows scenes from daily life, where objects are shown, moving with constant speed.
Vehicle on a country road
Gliding aeroplane
Ship in calm water
Motor boat on a river
Skydiver on an open parachute
A balloon floating in the wind
Bubbles raising in a liquid
Slider on an air-cushion track
The message of each of these videos is the same: If the sum of all applied forces cancel each other, so that the sum of all forces is zero, the object will move with constant speed.
