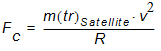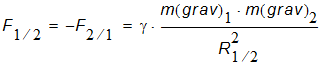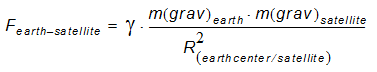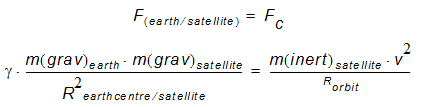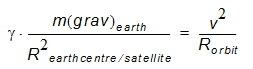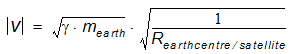back Home
6. Circular Motion
Newton´s 1st law reads as follows:
Every body remains in its state of rest, or uniform motion in a straight line, unless it is compelled to change that state by an applied force.
Important here is the word: "straight line". If a body does not move on a straight but on a curved line, its velocity is changing its direction. This is not possible without an applied Newtonian force, even if the object moves with constant speed.
For a homogeneous movement on a circular path, where the curvature is constant, the applied force F - named centripetal force - is directed in every moment towards the centre of the circle.For the force F, needed for an object to move with constant speed on a circular path the following relation can be derived from Newton´s 2nd law as:
-
F = m a = m v2/R1
m = inertial mass of the circulating object
R = radius of the circular path
|v| = constant amount of the velocity on the circular path.
The derivation of this equation can be found in any text book.
As already mentioned this force is called ,centripetal force". In every moment it is oriented towards the centre of the circular path.
What about the well-known ,centrifugal force" oriented towards the outside?
The following video poses an interesting question related to these two kinds of forces.

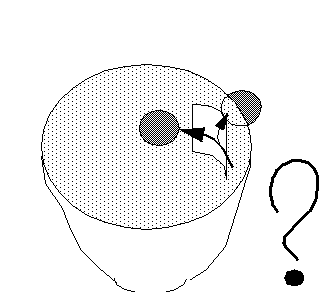
Fig 6.1.: Video "ball in a rotating beaker"
(Ball in a rotating beeker)
Will the ball stay inside or go outside, due to the so-called ,centrifugal force"?
More related information is found on the next pages.
6.2. Circulating Objects, Connected by an Elastic Spring
Fig 6.2.: Simulation "6-rotation-spring"
2 objects connected by a spring
Force of Inertia - Centrifugal Force
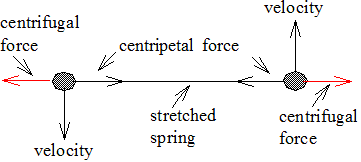
As always for acceleration processes, a force of inertia as acceleration-reaction force can be visualized (fig. 4.3 for all particles to be set; fig.4.4 for a selected particle already set).
For circulating movements this force is known as "centrifugal force".
Accelerated movement on a straight line can be interpreted as an equilibrium between a Newtonian and an acceleration-reaction force. The same is possible for movements on a curved path, in this case a circular path. In every moment the centrifugal force as an acceleration-reaction force F
a-r
is of equal strength as the centripetal force F
N
, a Newtonian force. Both forces act in the same direction but with opposite orientation:
>
F
N
= - F
a-r
or F
centripetal
= - F
centrifugal
Computation
To achieve a circular path of both particles this force has to correspond to the centripetal force F = m v 2 /R needed for each particle to circulate with a velocity |v| around a centre with radius R.
The force which the stretched spring applies on both particles can be determined by Hook´s law:
F
spring
= s D
(l 0 = rest length; l = actual length under tension; s = l - l 0 ; D = spring constant)
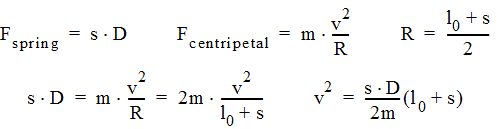
The settings in the simulation are (in corresponding units): l 0 =1500; s=100; m=2; D=1;
You may calculate the value for |v| for a circular orbit and compare it with the simulation.
For m ≠ 2 or for different spring parameters the relation given above for a circular motion is no longer valid. The orbit of the particles is no longer strictly circular.
Video ,Ball in a rotating Beaker"
In the experiment shown in the video above, the centripetal force on the ball is applied by the wall of the beaker and oriented towards the centre.
When the ball reaches the hole in the wall, this centripetal force disappears. The movement is no longer accelerated and so the centrifugal force - an acceleration-reaction force - also disappears. The ball will continue to move on a straight line.
If the width of the hole is not too large the ball will hit the opposite border of the hole from the inside and will stay inside of the beaker.
6.3. Objects Moving under Mutual Gravitational Attraction
The simulation "6-rotation-mutual-gravity" allows to study the situation where 2 particles are rotating on a circular path due to mutual gravitational attraction.
Fig 6.3.: Simulation "6-rotation mutual-gravity"
The corresponding velocity v circle for a circular orbit can be found by trial and error. The correct value (in suitable units) for the given situation is for the right particle v z = 100, for the left particle v z =-100.
The following computation shows how the velocity v circle , necessary for an exact circular orbit, can be determined.
Computation of v circle for a Uniform Circular Motion
Based on the general law of gravity and Newton´s 2nd law the following relation can be derived for the path velocity of 2 gravitating objects circulating around a common centre.
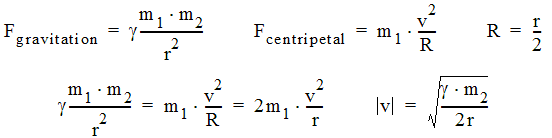
For the given simulation we have the following values (in corresponding units):
γ = 10 4 ; m 1 = m 2 = 10 3 ; R = 5 10 2 ; v = 100
The simulation "6-rotation mutual-gravity" demonstrates an agreement between computation and simulation?
6.4. Movement of an Object in the Coulomb Field of a Central Body
Material objects in space, like earth, moon, the planets, the stars in our galaxy a.o. are always rotating in one way or the other. The following pages show why such rotation is necessary for system of material objects to be stable in space.
The simulation "6-orbit-coulomb" shows a small ball circulating around an attracting central body (mass ratio 1:10 5 ). Due to this large ratio, the problem is very much simplified, because the movement of the large object is rather small and can be neglected. Both objects are charged with opposite polarity and are therefore attracting each other. The advantage of such a simulation becomes obvious if the effect of the inertial mass on the resulting orbit shall be studied
Fig 6.4.: How to set or change
the Coulomb and gravitational constant
In reality, when objects rotate around each other (like moon and earth) due to mutual gravitational interaction, it is not possible to change the attractive force independent of the mass of the objects. In the simulation above, however, the attracting force between the particle is simulated as a Coulomb force. Therefore such independent variation of attractive force and mass is possible. This allows to pose some interesting questions, which could lead to a deeper understanding of rotating objects unter mutual attraction.
Fig 6.5.: Simulation "6-orbit-Coulomb"
Interesting settings are (in suitable units):
6.5. Movement of an Object in the Gravitational Field of a Central Body
The simulation "6-orbit-gravity" shows a small ball circulating around a central body, attracted by gravity (mass ratio 1:106).
At start the velocity is set in such a way that the small body orbits on a circle.
Fig 6.6.: Simulation "6-orbit-gravity"
6.6. A Dropping Apple and the Circulating Moon - a Comparison
When an apple drops down from a tree it moves perpendicular to the surface of the earth. Taking the earth as a system of reference at rest, the moon is orbiting around the earth on a nearly perfect circular orbit. These two movements rely on the same basic law. In the following will be shown, where the difference is.
The simulation "6-compare-apple-moon" shows first a satellite above a central object, for instance the earth. Without a tangential velocity is drops down on a straight line towards the central body.
|
|
Fig 6.7.: Simulation "6-compare-apple-moon"
What kind of common aspect exists between the movement of an apple, dropping down from a tree and the movement of the moon, circulating the earth?
6.7. Circulating Satellites on Different Orbits
Fig 6.8.: Simulation "6-orbit-radius"
Computation
As always in mechanics F c and a R follow Newton's basic law: F c = m a radial .
For the relation between radial acceleration a
radial
, velocity |v| and radius of the orbit R we have:
a
radial =
v
2
/
R
.
For the centripetal force F c it follows that:
This necessary centripetal force is provided by the gravitational attraction between the satellite and the central body.The gravitational force is given by the universal law of gravity:
If applied to a satellite, surrounding a central object we get:
In doing so we refer to the fact that a spherical body (such as the earth) behaves to the outside as if all its mass is concentrated at its centre. The distance therefore must be taken from the centre of the central body.
Since the centripetal force, necessary for a circular orbit is realized by this gravitational force we get:
From the fact that inertial and gravitational mass are proportional and measured in equal units it follows:
With R centre of central object/satellite = R orbit and solving for v we get:
If velocity v
1
and radius R
1
for a specific orbit are known and if the velocity v
2
for a different radius R
2
needs to be calculated, we have: 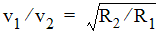 .
.
Example: From R
2
/R
1
= 2 follows: 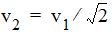 .
.
The simulation "6-orbit-radius" allows to check this computation by changing the distance between satellite and central object as well as the corresponding starting velocity of the satellite. Both parameters can be changed inside the "Particle Inspector" window.
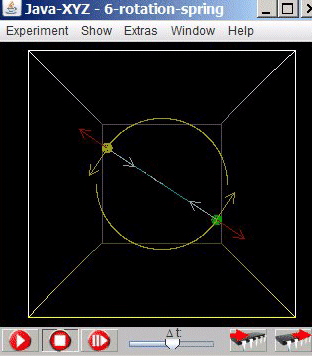 The simulation "6-rotation-spring" shows the movement of 2 particles, connected by a spring and circulating around a common centre.
The simulation "6-rotation-spring" shows the movement of 2 particles, connected by a spring and circulating around a common centre.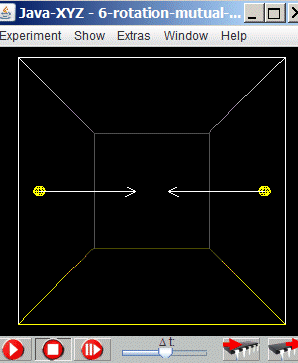 In the starting position the particles are at rest and will accelerate towards each other.
In the starting position the particles are at rest and will accelerate towards each other.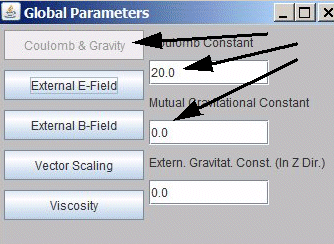 The charge of the particles cab be set in the "Particle Inspector" window.To simulation such an attraction a Coulomb constant has to be set to a certain value. This can be done in the "Global Parameter" window. In the same window the gravitational constant can be set.
The charge of the particles cab be set in the "Particle Inspector" window.To simulation such an attraction a Coulomb constant has to be set to a certain value. This can be done in the "Global Parameter" window. In the same window the gravitational constant can be set. 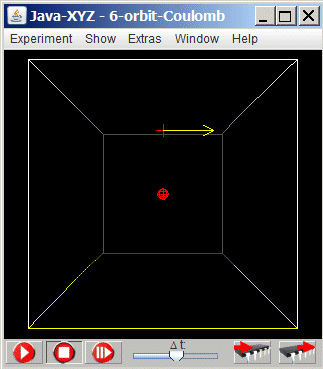 How will the orbit of the circulating body (in the simulation "6-orbit-Coulomb") change if either the centripetal force (charge q of the circulating object) - directed towards the centre - or its mass m or both will be changed, but each time independent from each other?
How will the orbit of the circulating body (in the simulation "6-orbit-Coulomb") change if either the centripetal force (charge q of the circulating object) - directed towards the centre - or its mass m or both will be changed, but each time independent from each other? 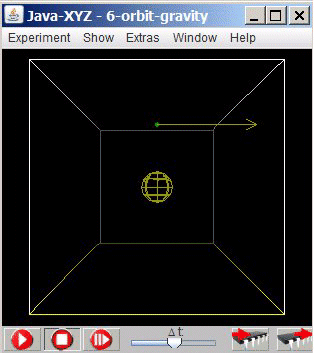 We can also say: The circulating body is attracted by the central body and should drop down towards the centre. However, due to its tangential velocity it is always missing it. Therefore the small object is permanently free falling.
We can also say: The circulating body is attracted by the central body and should drop down towards the centre. However, due to its tangential velocity it is always missing it. Therefore the small object is permanently free falling.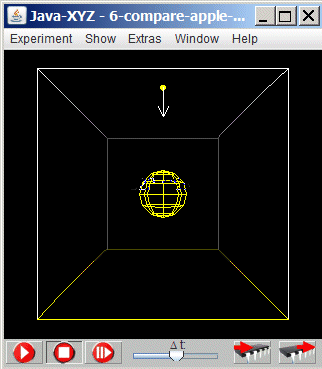 If the tangential velocity v
x
is increased stepwise, the satellite will move on kind of parabolic paths until it finally will start circulating on elliptic orbits with a circular orbit as special case
If the tangential velocity v
x
is increased stepwise, the satellite will move on kind of parabolic paths until it finally will start circulating on elliptic orbits with a circular orbit as special case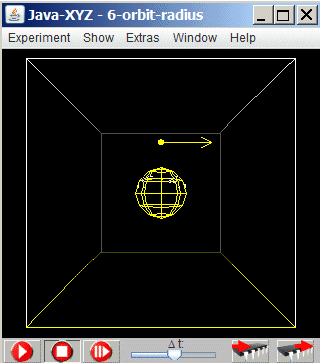 The simulation "6-orbit-radius" shows a satellite, with a starting velocity of 200 units, and a distance from the centre of the central objects of 400 units.
The simulation "6-orbit-radius" shows a satellite, with a starting velocity of 200 units, and a distance from the centre of the central objects of 400 units.